|
MAIN PAGE
> Back to contents
Arctic and Antarctica
Reference:
Galkin A., Plotnikov N.A.
Calculation of the coefficient of thermal conductivity of snow cover
// Arctic and Antarctica.
2023. ¹ 3.
P. 16-23.
DOI: 10.7256/2453-8922.2023.3.43733 EDN: VMDOVA URL: https://en.nbpublish.com/library_read_article.php?id=43733
Calculation of the coefficient of thermal conductivity of snow cover
Galkin Aleksandr
ORCID: 0000-0002-5924-876X
Doctor of Technical Science
Professor, Chief Researcher of the Melnikov Permafrost Institute SB RAS
677010, Russia, Yakutsk, ul. Merzlotnaya, 36, IMZ SO RAN. Laboratoriya geotermii kriolitozony

|
afgalkin@yandex.ru
|
|
 |
Other publications by this author
|
|
|
Plotnikov Nikolay Afanasievich
ORCID: 0000-0001-6013-931X
Melnikov Permafrost Institute SB RAS
677010, Russia, Republic of Sakha(Yakutia), Yakutsk, Permafrost str., 36

|
plotnikov-nikolay96@mail.ru
|
|
 |
|
DOI: 10.7256/2453-8922.2023.3.43733
EDN: VMDOVA
Received:
07-08-2023
Published:
19-10-2023
Abstract:
The aim of the work is to obtain generalized simple formulas for calculating the coefficient of thermal conductivity of snow cover when calculating its thermal resistance. To achieve the goal, a comparison was made of the parabolic formula of N.I. Osokin, obtained on the basis of generalization and correlation analysis of existing dependencies for calculating the coefficient of thermal conductivity having fractional coefficients, with its simplified version with integer coefficients. Based on the linearization of the base Simple linear formulas for determining the coefficient of thermal conductivity depending on the density of snow for two characteristic density ranges (200-300) and (300-400) kg/m3 were also obtained. The percentage errors in the calculations of the coefficient of thermal conductivity of snow, which are possible with the simplification of the coefficients and linearization of the basic parabolic dependence of the coefficient of thermal conductivity on the density of the snow cover, are determined. It is established that the errors arising from the linearization of the basic function do not exceed 5%, which is quite acceptable in engineering calculations. The discrepancy between the results of calculations according to the basic and simplified formula (with coefficients rounded to integer values of the first order) does not exceed 1.5% in the entire considered range of changes in snow density. The results of numerical calculations are presented in the form of graphs that allow you to visually assess the impact of simplifying the calculation formula and its linearization on the accuracy of determining the coefficient of thermal conductivity of snow cover.
Keywords:
snow reclamation, thermal resistance, mistake, accuracy, calculation, simplification, approximation, linearization of the function, snow, ground
This article is automatically translated.
You can find original text of the article here.
Introduction. Snow cover plays an important role in the formation of the temperature regime of the active layer of the heliothermozone [1,2,3,4,5]. The management of the thermal regime of the active soil layer with the help of snow, the so-called "snow reclamation" is widely used in various fields of industry and agriculture [6,7,8,9,10,11]. For example: during the construction of winter roads and river crossings in seasonal road construction in the North and ensuring their reliable operation; to preserve mountain ranges from deep freezing of rocks during open development of placer deposits; when restoring cryolithozone agricultural lands disturbed by thermokarst; to ensure soil fertility by reducing winter freezing and effective spring humidification. Although, in a narrower interpretation of this term, adopted in agriculture, snow reclamation is usually understood as "management of the water-thermal regime of the active soil layer in order to improve its characteristics and provide the necessary functions by influencing the snow cover" [2,6]. Ultimately, the essence of snow reclamation is the optimal management of the thermal resistance of the snow cover, which is achieved, depending on the purpose of snow reclamation, either by accumulation or by ramming snow on a certain area of the earth's surface or an engineering facility. The importance of accurately determining the thermal resistance of snow cover for the stability of soil bases is described in detail in [11,12,13,14]. The authors note that the main difficulty in calculating the thermal resistance of snow cover lies in a wide range of changes in the coefficient of thermal conductivity of snow, which significantly depends on such unstable climatic characteristics as thaws and frosts, wind load, solar radiation, daily temperature fluctuations, etc. This causes a "spatio-temporal variability of the thermal resistance of the snow cover", which was investigated by the authors of [16,17,18,19] for a number of districts of the Krasnoyarsk Territory and the Komi Republic. In the same works, the influence of the texture of snow cover and layers of deep frost on thermal resistance was estimated (using the example of Western Svalbard and the Moscow region). It is shown that without taking into account the stratigraphy of the snow cover, the value of thermal resistance can be one and a half times lower than the real one. At the same time, most researchers consider the average snow density for the considered period of the existence of the snow cover to be a complex indicator of all impacts on the snow cover, separately highlighting the periods of melting. The purpose of this work was to obtain simple formulas for calculating the thermal conductivity coefficient of snow cover when determining its thermal resistance. Method. To achieve the goal, we use the generalized formula of N.I.Osokin [16], obtained by summarizing the data and functional dependencies that were given in open literature sources (according to the authors of this work, they used more than twenty available calculation formulas in the analysis). The formula has the following form 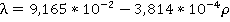 + 2,905 + 2,905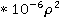 , , which we will present in a more convenient, in our opinion, form | k=(9,165-3,814j+2,905j^2)/100 | 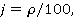 | (1) | here ?,k is the coefficient of thermal conductivity of snow, Vm/ mK; p is the average density of snow, kg/m3. The range of variation in the average density of snow, i.e. the range of application of the formula, is from 200 to 400 kg / m3. The density of snow is usually considered average in terms of the thickness of the snow cover. Note that not only in this paper, but also in many primary sources, regression coefficients are used when approximating experimental data with an accuracy of up to the third sign. At the same time, the authors forget that in reality, the third decimal place is the first sign in equation (1), since the value of the thermal conductivity coefficient of snow is determined up to the second decimal place. Therefore, without loss of accuracy, we can limit ourselves to only the first sign in the coefficients of the parabola and write down the formula given in [16] in the following simple and easy-to-remember form
| k=(9-4j+3j^2)/100, | 
| (2) | Sometimes, it is convenient to use linear functions for estimation calculations, so we will divide formula (1) into two intervals for snow density (200-300) and (300-400), kg/m3. Linearization of the parabolic function within these limits leads to the following linear relations for determining the thermal conductivity coefficient of snow cover | k=(11j-90)/100, k=(16j-24)/100 , | 2,0 ? j ? 3,0 3,0 ? j ? 4,0 | (3) (4) | The error of calculating the coefficient of thermal conductivity by approximate formulas (2) - (4), in comparison with the basic basic formula (1), is determined from the known ratio [20,21] Here k f is the coefficient of thermal conductivity determined by one of the formulas (2), (3) or (4), respectively. Results and discussion. For clarity, all quantitative results obtained by variant calculations according to the proposed formulas are presented in the form of graphs in Figures 1-3. Figure 1 shows a comparison of the values of the thermal conductivity coefficient calculated by formulas (1) and (2). 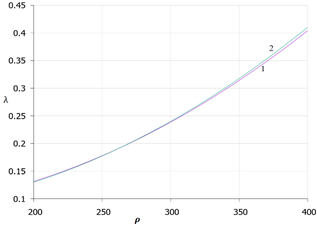
Fig. 1. The value of the thermal conductivity coefficient of snow depending on its density: 1 - calculated by formula (1); 2 - calculated by formula (2).
As can be seen from the graphs in the figure, the curves practically merge. That is, the difference in calculations, given that the coefficient of thermal conductivity of snow is determined with accuracy to the second sign, is insignificant. Indeed, if we consider the extreme point on the graph where the snow density (400 kg / m3) is maximum and corresponds visually to the maximum divergence of the curves, we get the following values of the thermal conductivity coefficient: according to the basic formula (curve 1) - 0.4039 W / mK; according to the proposed formula (curve 2) – 0.41 W / mK. The difference is 0.0061 W/mK or 1.5%. On all other sections of the density scale, these values will be even smaller. Thus, it becomes obvious that the use of the proposed formula (2) in calculations is expedient from an engineering point of view. Moreover, such a formula is easy for students and specialists to remember and does not require access to primary sources. The formula differs from the known dependencies in its compactness and simplicity. In the future, we will call this formula the "modified formula of N.I.Osokin". Figure 2 shows graphs comparing the basic formula (1) with linear formulas for two characteristic ranges of snow density variation: A) - (200-300) kg/m3 and B) - (300-400) kg/m3. A) B) 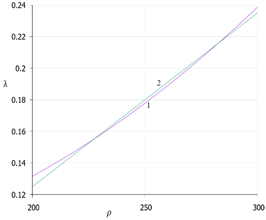 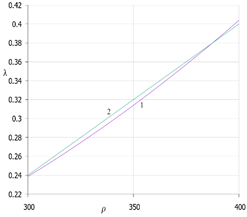
Fig.2. Values of the thermal conductivity coefficient of snow depending on its density: 1- calculated by the formula (1); 2 - calculated by the formula A) - (3) and B) - (4). It can be seen from the graphs that in this case the divergence of lines (1) and (2) is more significant. However, the degree of their discrepancy is visually not very large. Linearization is usually considered successful if the error in calculations for the basic and linearized functions does not exceed the values allowed in engineering practice, which is usually %. Figure 3 shows the curves characterizing the percentage errors in calculating the values of the thermal conductivity coefficient according to the proposed formulas compared with the values determined by the basic formula. The figure also confirms the expediency of dividing the density scale into two characteristic linearization sections. Without splitting into two sections, calculation errors based on linear dependencies can be significant and exceed a multiple of the error allowed in engineering practice for calculating design values (curves 1 and 2 in Fig. 3). 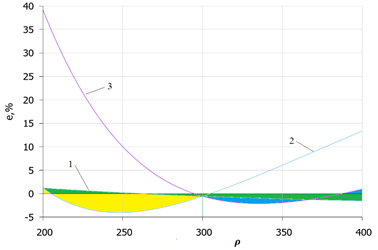
Fig. 3. Percentage error in calculating the heat transfer coefficient compared to the basic formula (1): 1 – when calculated by formula (2); 2 – when calculated by formula (3); 3 – when calculated by formula (4). At the same time, when the basic function is linearized in two separate sections, the maximum error does not exceed 4.5%. The areas of error variation from the linearization of the basic parabolic function are highlighted in yellow and blue in the figure. The area of error resulting from the replacement of fractional coefficients in equation (1) with integer values and the representation of the equation for determining the thermal conductivity of snow cover in the form of formula (2) is highlighted in green. The analysis shows that the maximum error does not exceed 1.5%. This is the basis for recommending the use of N.I.Osokin's formula in the proposed form for practical purposes.
Conclusion. The influence of the accuracy of setting coefficients in a parabolic function for determining the coefficient of thermal conductivity of snow depending on its density is investigated. It is shown that replacing fractional coefficients with integer values leads to a significant simplification of the type of functional dependence without loss of accuracy of the result obtained. A modified formula of N.I.Osokin is proposed, which is easy to memorize and operational estimates of the effect of snow density on the coefficients of thermal conductivity and thermal resistance of snow cover. Based on the linearization of the basic functional dependence, simple linear formulas were also obtained for determining the thermal conductivity coefficient depending on the density of snow for two characteristic density ranges (200-300) and (300-400) kg/m3. Percentage errors in the calculations of the thermal conductivity coefficient of snow were determined, which are possible when simplifying the coefficients and linearization of the basic parabolic dependence of the thermal conductivity coefficient on density of snow cover. It is established that errors arising during the linearization of the basic function do not exceed 4.5%, which is quite acceptable in engineering calculations. The discrepancy between the calculation results according to the basic and simplified formula (with coefficients rounded to integer values of the first order) does not exceed 2.3% in the entire range of snow density changes considered. The results of numerical calculations are presented in the form of graphs that allow us to visually assess the effect of simplifying the calculation formula and its linearization on the accuracy of determining the thermal conductivity coefficient of snow cover. The article has not only scientific, but also applied methodological significance and will be useful to students and postgraduates studying in the direction 1.6.7. "Engineering geology, permafrost and soil science". Further research in this area should be aimed at investigating the effect of the accuracy of determining the average snow density on the calculation of the thermal resistance of the snow cover.
References
1. Osokin, N.I., & Sosnovsky, A.V. (2016). Influence of thermal resistance of snow cover on the stability of permafrost. Cryosphere of the Earth. Vol. XX, No. 3, pp. 105–112. doi:10.21782/KZ1560-7496-2016-3(105-112)
2. Shulgin, A. M. (1967). Soil climate and its regulation. L.: Gidrometeoizdat.
3. Balobaev, V.T. (1991). Geothermia of the frozen zone of the lithosphere of the north of Asia. Novosibirsk: Nauka.
4. Pavlov, A.V. (1980). Calculation and regulation of the temperature regime of the soil. Novosibirsk: Science.
5. Khabibullin, I. L., & Soldatkin, M. V. (2012). Dynamics of freezing of the seasonal-thawed layer of the permafrost zone, taking into account the presence of snow cover. Bulletin of the Bashkir University, 17(2), 843-846.
6. Shulgin, A. M. (1986). Snow reclamation and soil climate. L.: Gidrometeoizdat.
7. Zheleznyak, I. I., & Sakisyan, R. M. (1987). Methods of management of seasonal freezing of soils in Transbaikalia. Novosibirsk: Nauka.
8. Galkin, A.F., & Pankov, V. Yu. (2022). Thermal Protection of Roads in The Permafrost Zone. Journal of Applied Engineering Science, 20(2), 395-399. doi:10.5937/jaes0-34379
9. Zhirkov, A., Sivtsev, M., Lytkin, V., Sezhurne, A., & Wen, Z. (2023). Assessment of the possibility of restoration and protection of the territories of Central Yakutia, Eastern Siberia disturbed by thermokarst. Land, 12(1), 197.
10. Pak, H., Fedorov, A.N., Zheleznyak, M.N., Konstantinov, N., & Walsh, J.E. (2015). Influence of snow cover on thermal regimes of permafrost in the Arctic. Climate Dynamics, 44, 2873–2895. doi:10.1007/s00382-014-2356-5
11. Zhirkov, A.F., & Sivtsev, M.A. (2022). Assessment of the possibility of restoring the protective layer in the conditions of Central Yakutia. In the collection: Monitoring in the permafrost zone. Collection of reports of the Sixth Conference of Geocryologists of Russia with the participation of Russian and foreign scientists, engineers and specialists (pp. 444-450). Moscow.
12. Galkin, A.F. (2022). Controlling The Thermal Regime of the Road Surface in the Cryolithic Zone. Transportation Research Procedia, 63, 1224-1228. Retrieved from https://doi.org/10.1016/j.trpro.2022.06.128
13. Pavlov, A.V. (2008). Monitoring of permafrost. Novosibirsk: "Geo".
14. Osokin, N.I., Sosnovsky, A.V., Nakalo,v P.R., & Nenashev, S.V. (2013). Thermal resistance of snow cover and its influence on soil freezing. Ice and snow, 53(1), 93–103.
15. Sosnovsky, A.V. (2006). Mathematical modeling of the influence of the thickness of the snow cover on the degradation of permafrost during climate warming. Cryosphere of the Earth, X(3), 83-88.
16. Osokin, N.I., Sosnovsky, A.V., Chernov, R.A., & Nakalov, P.R. (2014). Thermal resistance of snow cover and its variability. Cryosphere of the Earth, XVIII(4), 70–77.
17. Osokin, N.I., Sosnovsky, A.V., & Chernov, R.A. (2017). Coefficient of thermal conductivity of snow and its variability. Cryosphere of the Earth, XXI(3), 60–68.
18. Osokin, N.I., Sosnovsky, A.V., & Chernov, R.A. (2013). Influence of stratigraphy of snow cover on its thermal resistance. Ice and Snow, 53(3), 63–70. doi:10.15356/2076-6734-2013-3-63-70
19. Kotlyakov, V.M., Sosnovsky, A.V., & Osokin, N.I. (2018). Estimation of the coefficient of thermal conductivity of snow by its density and hardness in Western Spitsbergen. Ice and Snow, 58(3), 343–352. doi:10.15356/2076-6734-2018-3-343-352
20. Galkin, A.F., Pankov, V.Yu., & Fedorov, Y.V. (2022). Calculated coefficient of thermal conductivity of a binary mixture. Arctic and Antarctic, 4, 11-19. doi:10.7256/2453-8922.2022.4.39349
21. Galkin, A.F., Pankov, V. Yu., & Zhirkova, E.O. (2023). Thermal Conductivity of a Gravel Layer of a Road. E3S Web of Conferences 371, 03042. Retrieved from https://doi.org/10.1051/e3sconf/20233710304
Peer Review
Peer reviewers' evaluations remain confidential and are not disclosed to the public. Only external reviews, authorized for publication by the article's author(s), are made public. Typically, these final reviews are conducted after the manuscript's revision. Adhering to our double-blind review policy, the reviewer's identity is kept confidential.
The list of publisher reviewers can be found here.
The subject of the study is the study of options for obtaining simple formulas for calculating the thermal conductivity coefficient of snow cover when determining its thermal resistance. The research methodology consisted in the search and description of various methods and the choice of a generalized formula proposed by N.I.Osokina to achieve the goal, which is a very valuable contribution to the development of the methodology for studying heat exchange processes between the atmosphere and the lithosphere in snowy conditions. The authors of the methodology proposed a modification of the N.I.Osokin formula, which is easy to remember from a methodological point of view and easy to use in operational assessments of the effect of snow density on the coefficients of thermal conductivity and thermal resistance of snow cover. The author also obtained simple linear formulas for determining the coefficient of thermal conductivity depending on the density of snow for two characteristic density ranges (200-300) and (300-400) kg/m3 based on the linearization of the basic functional dependence. He determined percentage errors in calculations of the coefficient of thermal conductivity of snow, which are possible when simplifying the coefficients and linearization of the basic parabolic dependence of the coefficient of thermal conductivity on the density of snow cover. The level of error that occurs during the linearization of the basic function has been established, which does not exceed 4.5%, which is quite acceptable in engineering calculations and does not significantly affect the subsequent result. The relevance of the study consists in the systematization of research methods. The results of statistical and mathematical numerical calculations presented in the form of graphs make it possible to visually reflect and evaluate the impact of simplifying the calculation formula and its linearization on the accuracy of determining the thermal conductivity coefficient of snow cover. The article, having scientific significance, can also perform a great practical useful service, since it has great and applied methodological significance and will be useful to students and postgraduates studying in the direction 1.6.7. "Engineering geology, permafrost and soil science". Further prospective research in this area should be aimed at investigating the effect of the accuracy of determining the average snow density and their effect on the calculation of the thermal resistance of the snow cover. The scientific result consists in modifying the available methods for calculating the thermal conductivity of snow cover by optimizing the calculation formulas. The practical significance is determined by the ease of use, simplicity of application and the ability to easily operate the proposed methodological apparatus for calculating the thermal conductivity of snow cover in the study of thermodynamic processes of the atmosphere or lithosphere, as well as during winter hibernation. The obtained data can be applied in practice at the objects of assessment of thermidynamic processes. Style, structure, content The style of presentation is good, (does not) require edits, abbreviations. The tables are informative. The figures are acceptable, they do not repeat the contents of the tables. The author of the article uses numerous illustrations in the form of drawings and graphs reflecting dependencies. The bibliography is extensive and exhaustive. An adequate modern list of references has been used. There are references to literary sources in the text. The appeal to the opponents consists in references to the literary sources used. Conclusions, the interest of the readership is undeniable. The conclusions are sufficiently reasoned, substantiated, and exhaustive. It may be useful for practitioners to implement, as well as for students and postgraduates studying in the direction 1.6.7. "Engineering geology, permafrost and soil science".
Link to this article
You can simply select and copy link from below text field.
|
|



