|
MAIN PAGE
> Back to contents
Space Research
Reference:
Zhang L., Zhao R., Ma M.
Black hole entropy in the Reissner-Nordström-de Sitter model
// Space Research.
2017. № 1.
P. 5-9.
DOI: 10.7256/2453-8817.2017.1.21538 URL: https://en.nbpublish.com/library_read_article.php?id=21538
Black hole entropy in the Reissner-Nordström-de Sitter model
Chzhan Li-Chun
Doctor of Physics and Mathematics
Professor at the Department of Physics of the Institute of Theoretical Physics of Shanxi Datong University
037009, China, Datong

|
ms_ma@sxdtdx.edu.cn
|
|
 |
Chzhao Zhen'
Doctor of Physics and Mathematics
Institute of Theoretical Physics of Shanxi Datong University
037009, China, Datong

|
ms_ma@sxdtdx.edu.cn
|
|
 |
|
Ma Meng-Sen
Doctor of Physics and Mathematics
Faculty of Physics, Institute of Theoretical Physics, Shanxi Datong University
037009, China, Datong

|
mengsenma@gmail.com
|
|
 |
|
DOI: 10.7256/2453-8817.2017.1.21538
Received:
25-12-2016
Published:
08-02-2017
Abstract:
The paper studies the development of the macroscopic methods of high-energy physics analysis. The authors consider the evolution of black holes within the phenomenological approach, analogous to classical thermodynamics, in which the black hole area determines its entropy, and the surface gravitation, correspondingly, - the temperature, in the framework of the relativist cosmological model (de Sitter universe). The research subject is the ways of calculation of effective thermodynamic properties of black holes. To calculate a black hole entropy, the authors apply the event horizon and cosmological horizon interdependence hypothesis. To accomplish the research task, the authors apply the system and structural-functional approaches, the methods of cosmology, relativistic mechanics and Einstein’s geometric theory of gravitation, in particular, the exact solutions of the Einstein field equations with the cosmological constant for the Reissner- Nordström metric for the space-time description. The authors find the analytical solution for the calculation of the total entropy of a spherically symmetric charged black hole in the Reissner- Nordström model for de Sitter universe. The paper shows that the expression for entropy includes not only the sum of entropies of the event horizon and cosmological horizon of the black hole, but also the additional term, taking into account their entanglement. The obtained results of black hole thermodynamics extend the analogy with the first law of thermodynamics, thus broadening the applicability of the approach to the cosmological studies.
Keywords:
Theoretical Physics, Cosmology, General relativity theory, de Sitter space, Reissner–Nordström metric, Black holes Physics, Event horizon, Cosmological horizon, Entropy, Surface gravity
The astronomical observations show that our Universe is probably approaching de Sitter one [1-4]. However, as is well known that in de Sitter space there is no spatial infinity and no asymptotic Killing vector which is globally timelike [5]. Moreover, black holes in de Sitter space cannot be in thermodynamic equilibrium in general. Because there are multiple horizons with different temperatures for de Sitter black holes. To overcome this problem, one can analyze one horizon and take another one as the boundary or separate the two horizons by a thermally opaque membrane or box [6-7]. In this way, the two horizons can be analyzed independently. Besides, one can also take a global view to construct the globally effective temperature and other effective thermodynamic quantities [8-9]. No matter which method is used, the total entropy of de Sitter black hole is supposed to be the sum of both horizons, namely S=Sb+Sc[10].
We think that the truth may be not so simple because the event horizon and the cosmological horizon are not independent. There may exist some correlations between them due to the following considerations. We can take the Reissner–Nordström–de Sitter (RNdS) black hole as example. There are first laws of thermodynamics for both horizons. According to [11], the first laws for the black hole horizon and the cosmological horizon are respectively:
|
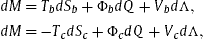
|
(1)
|
 where M is the conserved mass in dS space, Φ and Q stand for the electric potential and electric charge, and Λ is the cosmological constant. Including the variable Λ, the above first laws can have corresponding Smarr formulae, which are also given in [11]. The two laws in Eq. (1) are not truly independent. They depend on the same quantitiesM, Q, Λ. All the geometric and thermodynamic quantities for the both horizons can be represented by M, Q, Λ. Therefore, the size of black hole horizon is closely related to the size of the cosmological horizon, and the evolution of black hole horizon will lead to the evolution of the cosmological horizon. where M is the conserved mass in dS space, Φ and Q stand for the electric potential and electric charge, and Λ is the cosmological constant. Including the variable Λ, the above first laws can have corresponding Smarr formulae, which are also given in [11]. The two laws in Eq. (1) are not truly independent. They depend on the same quantitiesM, Q, Λ. All the geometric and thermodynamic quantities for the both horizons can be represented by M, Q, Λ. Therefore, the size of black hole horizon is closely related to the size of the cosmological horizon, and the evolution of black hole horizon will lead to the evolution of the cosmological horizon.
Considering the correlation or entanglement between the event horizon and the cosmological horizon, the total entropy of the RNdS black hole is no longer simplyS=Sb+Sc, but should include an extra term from the contribution of the correlations of the two horizons.
The line element of the RNdS black holes is given by
|
ds2=−h(r)dt2+h(r)−1dr2+r2dΩ2,
|
(2)
|

where
|
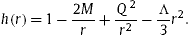
|
(3)
|
 There are three positive real roots for h(r)=0. The smallest one r− is the inner/Cauchy horizon, the intermediate one r+ is the event horizon of black hole and the largest one is the cosmological horizon. There are three positive real roots for h(r)=0. The smallest one r− is the inner/Cauchy horizon, the intermediate one r+ is the event horizon of black hole and the largest one is the cosmological horizon.
Generally, the temperatures at the event horizon and cosmological horizon are not equal. Thus, the whole RNdS system cannot be in equilibrium thermodynamically. However, there are two special cases for the RNdS black hole, in which the temperatures at the both horizons are the same. One case is the so-called Nariai black hole, the other is the lukewarm black hole [12-15]. For the Nariai black hole, the event horizon and cosmological horizon coincide apparently and have the same temperature, zero or nonzero [16].
Considering the connection between the black hole horizon and the cosmological horizon, we can derive the effective thermodynamic quantities and corresponding first law of black hole thermodynamics*:
|
dM=TeffdS−PeffdV+ϕeffDq
|
(4)
|
______________
* One can also take the cosmological constant Λ as the pressure and then derive the effective volume. In this case the effective first law should be: dM=TeffdS+ϕeffdQ+VeffdP. This has been done in another paper.

Here the thermodynamic volume is that between the black hole horizon and the cosmological horizon, namely
|
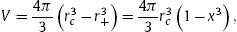
|
(5)
|
 where x=r+/rc. where x=r+/rc.
The total entropy can be written as
|
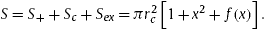
|
(6)
|
 Here the undefined function f(x) represents the extra contribution from the correlations of the two horizons. Then, how to determine the function f(x)? Here the undefined function f(x) represents the extra contribution from the correlations of the two horizons. Then, how to determine the function f(x)?
In general cases, the temperatures of the black hole horizon and the cosmological horizon are not the same, thus the globally effective temperature Teff cannot be compared with them. However, in the special case, such as lukewarm case, the temperatures of the two horizons are the same. We conjecture that in this special case the effective temperature should also take the same value. On the basis of this consideration, we can obtain the information of f(x).
According to Eq. (4), the effective temperature can be derived by
|
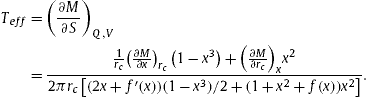
|
(7)
|
 From Eq. (3), one know that From Eq. (3), one know that
|
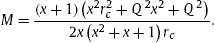
|
(8)
|
 We can derive the effective temperature We can derive the effective temperature
|
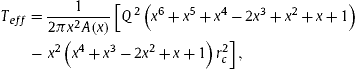
|
(9)
|
 where where
|
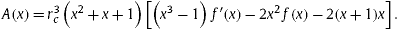
|
(10)
|

In the lukewarm case, there is
|
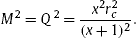
|
(11)
|
With this, we can obtain the effective temperature of lukewarm RNdS black hole:
|
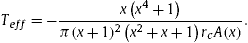
|
(12)
|
We also know that for the lukewarm RNdS black hole, the temperature is
|
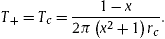
|
(13)
|
Equating the two temperatures, we obtain a differential equation for f(x):
|
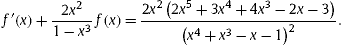
|
(14)
|
 Fortunately, this equation has analytic solution, which is Fortunately, this equation has analytic solution, which is
|
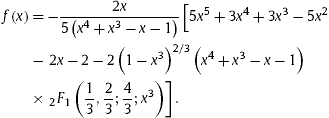
|
(15)
|
In Fig. 1, we depict the effective temperature Teff and S as functions of x . It is shown that Teff tends to zero as x→1, namely the charged Nariai limit. Although this result does not agree with that of Bousso and Hawking [13], it is consistent with the entropy. As is depicted in Fig. 1(b), the entropy will diverge as x→1. Besides, one can see the entropy is monotonically increasing with the increase of x , while Teff first increases and then decreases. According to the general definition of heat capacity,  , only in the region of x with positive temperature and positive slope the RNdS black hole can be thermodynamically stable. This is unexpectable. This means when the black hole horizon and the cosmological horizon are too far away (small x) or too close (large x), RNdS black hole cannot be thermodynamically stable. , only in the region of x with positive temperature and positive slope the RNdS black hole can be thermodynamically stable. This is unexpectable. This means when the black hole horizon and the cosmological horizon are too far away (small x) or too close (large x), RNdS black hole cannot be thermodynamically stable.
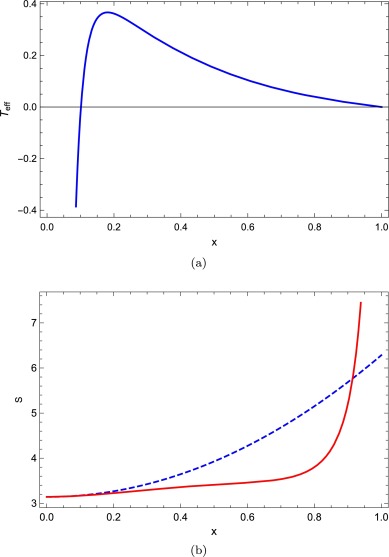
Fig. 1. Teff and total entropy S with respect to x. In (a), Teff has a maximum at x = 0.181. In (b), the dashed (blue) curve represents the sum of the two horizon entropies and the solid (red) curve depicts the result in Eq. (6). We set rc = 1 and Q = 0.1.
In this letter, we have presented the entropy of RNdS black hole. It is not only the sum of the entropies of black hole horizon and the cosmological horizon, but also with an extra term from the correlation between the two horizons. This idea has twofold advantages. First, if without the extra term in the total entropy, the effective temperature is not the same as that of the black hole horizon and the cosmological horizon in the lukewarm case. This is not satisfactory. Second, the method of effective first law of thermodynamics lacks physical explanation or motivation. While taking advantage of the method, we obtain the corrected entropy of RNdS black hole, which may make the method more acceptable.
Acknowledgements
This work is supported in part by the National Natural Science Foundation of China under Grant No. (11475108) and by the Doctoral Sustentation Fund of Shanxi Datong University (2011-B-03).
References
1. A.G. Riess, et al. Astron. J., 116 (1998), p. 1009.
2. S. Perlmutter, et al.Astrophys. J., 517 (1999), p. 565.
3. A.G. Riess, et al. Astrophys. J., 536 (2000), p. 62.
4. A.G. Riess, et al. Astrophys. J., 560 (2001), p. 49.
5. V. Balasubramanian, J. de Boer, D. Minic Phys. Rev. D, 65 (2002), Article 123508.
6. A. Gomberoff, C. Teitelboim Phys. Rev. D, 67 (2003), Article 104024.
7. Y. Sekiwa Phys. Rev. D, 73 (2006), Article 084009.
8. M. Urano, A. Tomimatsu Class. Quantum Gravity, 25 (2009), p. 105010, arXiv:0903.4230.
9. H.H. Zhao, L.C. Zhang, M.S. Ma, R. Zhao Phys. Rev. D, 90 (2014), Article 064018.
10. D. Kastor, J. Traschen Phys. Rev. D, 47 (1993), p. 5370.
11. B.P. Dolan, D. Kastor, D. Kubiznak, R.B. Mann, J. Traschen Phys. Rev. D, 87 (2013), Article 104017. arXiv:1301.5926.
12. L.J. Romans Nucl. Phys. B, 383 (1992), p. 395.
13. D. Kastor, J. Traschen Class. Quantum Gravity, 13 (1996), p. 2753.
14. R.G. Cai, J.Y. Ji, K.S. Soh Class. Quantum Gravity, 15 (1998), p. 2783.
15. B.B. Wang, C.G. Huang Class. Quantum Gravity, 19 (2002), p. 2491.
16. R. Bousso, S. Hawking Phys. Rev. D, 54 (1996), p. 6312.
Link to this article
You can simply select and copy link from below text field.
|
|



