MAIN PAGE
> Back to contents
Cybernetics and programming
Reference:
Grishentsev A.Y., Korobeinikov A.G., Yuganson A.N.
Computational optimization of mutual transformations of color spaces based upon the arithmetic fixed-point.
// Cybernetics and programming.
2017. № 4.
P. 84-96.
DOI: 10.25136/2644-5522.2017.4.24005 URL: https://en.nbpublish.com/library_read_article.php?id=24005
Computational optimization of mutual transformations of color spaces based upon the arithmetic fixed-point.
Grishentsev Aleksei Yur'evich
Doctor of Technical Science
Associate Professor, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49

|
grishentcev@ya.ru
|
|
 |
Other publications by this author
|
|
Korobeinikov Anatolii Grigor'evich
Doctor of Technical Science
professor, Pushkov institute of terrestrial magnetism, ionosphere and radio wave propagation of the Russian Academy of Sciences St.-Petersburg Filial
199034, Russia, g. Saint Petersburg, ul. Mendeleevskaya, 1

|
Korobeynikov_A_G@mail.ru
|
|
 |
Other publications by this author
|
|
|
Yuganson Andrei Nikolaevich
graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, Saint Petersburg, Kronverkskii prospekt, 49

|
a_yougunson@corp.ifmo.ru
|
|
 |
Other publications by this author
|
|
|
DOI: 10.25136/2644-5522.2017.4.24005
Received:
25-08-2017
Published:
17-09-2017
Abstract:
In their article the authors provide their results on systematization of methods for computational optimization of the transformation of color spaces based upon the application of fixed-point arithmetic. The authors formulate the goals and analyze the key problems arising in the situation of computational optimization in the process of color space formation from the standpoint of the speed of operation increase. The principles of transition from a floating point format to a format with a fixed point are stated. The authors also provide an example for the analysis of computational optimization for the mutual transformation of RGB and Y709CbCr. In this article the authros consider the method of computational optimization of the transformation of color spaces based on the application of fixed-point arithmetic. When applying the considered principle of practical implementation, the computation time for an image of 4134x2756 on an Intel Core 2 Duo processor becomes 18 times less. This is a very significant increase in productivity. It is not too difficult to apply this approach to other similar calculations, especially on modern 64-bit and 128-bit processors, when the necessary values fit into a single processor register.
Keywords:
parallel processing of images, serial processing of images, mathematical coprocessor, computing optimization, the format with fixed point, format with a floating point, RGB, transformation, color space, image processing
This article written in Russian. You can find original text of the article here
.
Введение
Существует значительное многообразие цветовых пространств
позволяющих отображать цветовую палитру графического изображения. Поэтому при преобразованиях
форматов графических данных часто приходится иметь дело с преобразованиями
цветовых пространств. В большинстве случаев пользователю желательно иметь
быстрый, приводящий к минимальным искажениям алгоритм преобразования. Исследованиями
и стандартизацией, в том числе, в области цветоощущения, цветопередачи,
занимаются ряд организаций по всему миру. Данные организации разработали ряд
стандартов и рекомендаций по классификации и использованию цветовых
пространств, например [1-3].
Анализ литературы и открытой
документации к некоторым программным средствам показал, что уделено не
достаточное внимание вопросам вычислительной оптимизации алгоритмов
преобразования цветовых пространств [3-11].
В подавляющем большинстве случаев преобразования рассматриваются в форматах с
плавающей точкой, что собственно вызывает ряд вопросов при практическом
внедрении, например, с учётом значительных размеров современных цифровых
графических изображений, преобразования цветовых пространств в форматах с
плавающей точкой, даже с учётом использования математического сопроцессора (FPU от англ. floating point
unit), требует существенных вычислительных затрат. При использовании арифметики
с плавающей точкой существенное повышение скорости вычислений может
предоставить применение графических сопроцессоров на базе библиотек OpenGL, DirectX или
технологии неграфических вычислений на базе графических сопроцессоров GPGPU (от
англ. General-purpose graphics processing units), но применение специальных
средств обработки цифровой графической информации не всегда доступно и
целесообразно. Но следует отметить, что многие современные приложения обработки
изображений реализованы в системах, не имеющих GPU, примером таких систем могут быть
системы на базе микроконтроллеров STM32 (http://www.st.com/) реализующие методы обработки
динамических (в том числе видео) и статических изображений и другие подобные
системы. Таким, образом, кроме параллельной, по-прежнему являются актуальными
методы последовательной обработки изображений. Рассмотренные в статье методы
могут быть использованы как в системах параллельной, так и в системах
последовательной обработки изображений.
Фиксированная точка вместо плавающей
На рис. 1 приведено две схемы обработки сигналов в соответствии с
последовательностью преобразований. Схема на (рис. 1, а) обеспечивает высокое
быстродействие, но накладывает некоторые, порой недопустимые, ограничения на
процедуру преобразования. Схема на (рис. 1, б), позволяет производить самые
разнообразные цифровые преобразования сигнала, но существенно снижает
быстродействие на этапах: обработки сигнала в формате с плавающей точкой (ПТ) и
преобразования форматов.
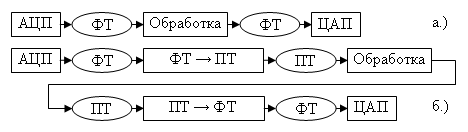
Рис. 1. Возможные схемы обработки цифровых сигналов. Обозначения:
ФТ – формат с фиксированной точкой; ПТ – формат с плавающей точкой; АЦП –
аналогово-цифровой преобразователь; ЦАП – цифро-аналоговый преобразователь; ФТ
→ ПТ и ПТ → ФТ – соответствующие преобразования форматов
Возможным компромиссом и решением проблемы повышения быстродействия,
является использование схемы, приведённой на (рис. 2). В данной схеме
отсутствуют операции в формате ПТ. Все операции выполняются в целочисленных
форматах, а требуемая точность достигается за счёт увеличения числа разрядов,
фактически за счёт перехода к формату с фиксированной точкой (ФТ).
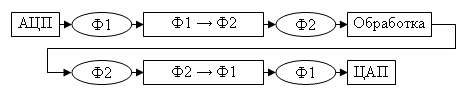
Рис. 2. Альтернативная схема цифровых преобразований сигналов.
Обозначения: Ф1 – ФТ формат, совместимый с ЦАП и АЦП; Ф2 – ФТ формат,
позволяющий произвести требуемые преобразования без переполнения
Например, в большинстве цветовых схем на каждый цветовой канал
изображения выделяется восемь бит. Сложение двух или более восьмибитных
элементов в формате типа unsigned char (или unsigned int8 – 8 бит без знака
0…255), может привести к переполнению и результату не соответствующему
ожиданиям. Использование переменных большей разрядности позволяет
гарантированно, не вызывая переполнения (до определённого значения суммы),
производить сложение. Например, формат unsigned int16 (16 бит без знака 0…65535) позволяет
произвести сложение, гарантированно не вызывая переполнения, до 256 элементов
типа unsigned char.
Следующая операция – умножение. В целочисленной арифметике умножение
на число, кратное степени двух, может быть выполнено с помощью поразрядного сдвига
влево. Умножение может достаточно быстро приводить к переполнениям. Например,
при операциях над сигналами, каждый дискретный элемент, которых представлен в
формате unsigned char, действия в формате unsigned int16 могут, в наихудшем
случае, вызвать переполнение уже при втором умножении в формате unsigned int32
– при четвёртом умножении. Можно заключить, что при использовании целочисленных
форматов, для операции умножения, необходимо учитывать возможность
переполнения, ограничивая результаты операции после выполнения соответствующего
числа раз. Практическая реализация такого ограничения зависит от особенностей
конкретной программно-аппаратной платформы и способа решения задачи.
Наиболее затратной с точки зрения потребления вычислительных
ресурсов, является – деление. В целочисленной арифметике деление на число,
кратное степени двух, может быть выполнено с помощью поразрядного сдвига
вправо. Заметим, что деление на любое число (кроме нуля) можно с заданной
степенью точности, реализовать с помощью операций сдвига и сложения. При
делении в целочисленной арифметике может возникать существенная потеря точности
за счёт отбрасывания дробной части.
 Обобщим сказанное в формальной записи.
Наиболее используемыми операциями цифровой обработки является умножение с
последующим суммированием, например: свёртка, БПФ, фильтр скользящего среднего
и др. реализуется на базе умножения с последующим суммированием [11-13].
Пусть по схеме (рис.2) в формате ФТ необходимо выполнить умножение (1) с
последующим суммированием Обобщим сказанное в формальной записи.
Наиболее используемыми операциями цифровой обработки является умножение с
последующим суммированием, например: свёртка, БПФ, фильтр скользящего среднего
и др. реализуется на базе умножения с последующим суммированием [11-13].
Пусть по схеме (рис.2) в формате ФТ необходимо выполнить умножение (1) с
последующим суммированием 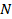 некоторых значений некоторых значений 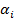 на коэффициенты на коэффициенты 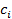 : :
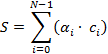
(1)
где 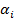 – в формате ФТ; – в формате ФТ; 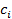 – в формате ПТ; – в формате ПТ; 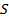 – результат суммы в формате ПТ. – результат суммы в формате ПТ.
Для исключения переполнения, в худшем случае, когда все значения 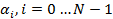 имеют максимально возможную величину,
необходимо: имеют максимально возможную величину,
необходимо:
– ограничить число элементов, т.е. N;
– ограничить значения коэффициентов 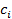 . .
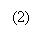 Ограничение величины N при
необходимости реализуется с помощью разделения всей суммы (1) на некоторые частичные
суммы: Ограничение величины N при
необходимости реализуется с помощью разделения всей суммы (1) на некоторые частичные
суммы:
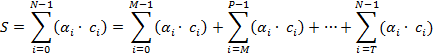
, (2)
где 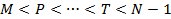 . .
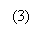 Ограничить значения Ограничить значения 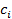 коэффициентов возможно, например, при помощи
нормирования: коэффициентов возможно, например, при помощи
нормирования:
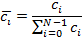
, (3)
причём нормирование целесообразно производить заранее, перед
обработкой.
Далее, с учётом формата ФТ в котором будет производиться умножение с
суммированием, необходимо принять решение: сколько знаков после точки должны
быть учтены. Пусть значимое число знаков будет k тогда
коэффициент h возможно
вычислить как h=0x10k=1016k=16k, где 0x – префикс 16-ричной системы исчисления. Основание степени
16 обеспечивает некоторую избыточность, по сравнению с основанием десятичной
системы счисления, что повышает точность вычислений. Если при основании 16 есть
вероятность переполнения, то в качестве основания, возможно, взять число 8, но
при этом произойдёт понижение точности. В общем случае при значении
коэффициента h=2k (2 в степени k,
где k – целое) операции
умножения и деления на h легко выполнить с помощью сдвига, влево и вправо на log2h бит соответственно, для
h=16k, логарифм имеет
значение: log2h=log224k, например:
– умножение: 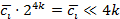 ; ;
– деление: 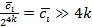 ; ;
где 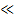 и и 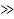 – операторы поразрядного сдвига влево и вправо
соответственно. Ценность выбора основания два заключается в возможности замены
в двоичных системах относительно медленных операций умножения и деления,
быстрыми операциями поразрядного сдвига. – операторы поразрядного сдвига влево и вправо
соответственно. Ценность выбора основания два заключается в возможности замены
в двоичных системах относительно медленных операций умножения и деления,
быстрыми операциями поразрядного сдвига.
Результирующее выражение для операций умножения с последующим
суммированием, возможно, осуществить в соответствии с выражением:
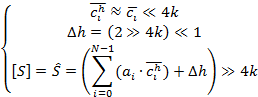
(4)
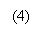 где где 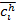 – целочисленный эквивалент коэффициента с
плавающей точкой – целочисленный эквивалент коэффициента с
плавающей точкой 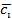 , ,
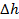 – поправочный коэффициент для округления к
ближайшему целому при делении с помощью сдвига. – поправочный коэффициент для округления к
ближайшему целому при делении с помощью сдвига.
Наиболее затратной, с точки зрения потребления вычислительных
тактов, является операция деления, как видно из выражения (4) операция деления,
при вычислении преобразования форматов по основанию кратному степени двойки,
заменяется операцией сдвига.
Взаимные преобразования цветовых пространств
Рассмотрим выражения для взаимных преобразований широко
используемых в практике цифровой обработки изображений цветовых пространств RGB и
Y709CbCr. Цветовое пространство RGB ассоциировано со
спецификой устройства зрительного анализатора человека, применяется для
визуализации изображений и как цветовое пространство некоторых графических
форматов, например BMP24.
Цветовое пространство Y709CbCr [2]
является вариацией цветоразностной модели YCbCr, применяется с системах цифрового телевиденья высокой
чёткости, а так же в некоторых форматах компрессии изображений [11,12].
Взаимные преобразования RGB и Y709CbCr осуществляются
при помощи уравнений:

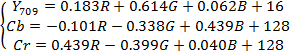
(5)
 и и
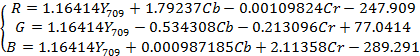
(6)
Вычислительная оптимизация на примере взаимных преобразований
цветовых пространств RGB и Y709CbCr
Для хранения изображений будем использовать массив структур, описание
структуры приведено в листинге 1.
Листинг 1. Структура вектора цветового пространства RGB и Y709CbCr (C++)
typedef unsigned
char uchar; // без знаковый байт
#pragma pack (push, 1)
// отключаем выравнивание памяти
// цветовая палитра RGB
// покомпонентное представление, в скобках указаны компоненты
// палитр (RGB) и (YCbCr)
соответственно
struct ColorSpace {
uchar byteLo; // компонента
младший байт (Lower) (R) (Y)
uchar byteAv; // компонента
средний байт (Average) (G) (Cb)
uchar byteHi; // компонента
старший байт (Hight) (B) (Cr)
};
#pragma pack (pop) //
выравнивание памяти исходное состояние
В листинге 2 приведён пример преобразования элемента изображения
(пикселя) из цветового пространства RGB в Y709CbCr
в формате ПТ.
Листинг 2. Преобразование значения из цветового пространства RGB в
Y709CbCr, вычисления в формате ПТ
(C++).
ColorSpace x; // пиксель типа ColorSpace (листинг 1)
float R, G, B; //
временные переменные
R=(float)x.byteLo; // цветовые
компоненты преобразуем в формат ПТ
G=(float)x.byteAv;
B=(float)x.byteHi;
// компонент Y
x.byteLo=(uchar)floor(0.183*R+0.614*G+0.062*B+16);
// компонент Cb
x.byteAv=(uchar)floor(-0.101*R-0.338*G+0.439*B+128);
// компонент Cr
x.byteHi=(uchar)floor(0.439*R-0.399*G-0.040*B+128);
Оптимизированный вариант преобразования данных из цветового
пространства RGB в Y709CbCr в соответствии с выражением (5),
(листинг 3), на базе принципов целочисленных вычислений в формате с ФТ рассмотренных
ранее. Для перевода в формата ФТ использовался множитель h=220=2(4)∙5=1048576
из расчёта максимального использования разрядной сетки, с целью повышения
точности, без переполнения. Для округления к ближайшему целому, возможно,
использовать добавление величины (0.5h)=(h>>1)=524288.
В листинге 3 и 4 для наглядности производимых действий некоторые операции
записаны излишне подробно. При включении оптимизации, большинство современных компиляторов
автоматически рассчитает все возможные значения на этапе компиляции и избавит
результирующий код от излишних действий.
Листинг 3. Преобразование значения из цветового пространства RGB в YCbCr, вычисления в формате ФТ (C++).
ColorSpace x; // пиксель типа ColorSpace
int R, G, B;
R=(int)x.byteLo;
G=(int)x.byteAv;
B=(int)x.byteHi;
const int h=((2<<20)>>1);
// h=524288;
// компонент (Y)
x.byteLo=(uchar)(abs(191889*R+643826*G+65012*B+16777216+h))>>20);
// компонент (Cb)
x.byteAv=(uchar)(abs(-105906*R-354419*G+460325*B+134217728+h)>>20);
// компонент (Cr)
x.byteHi=(uchar)(abs(460325*R-418382*G-41943*B+134217728+h)>>20);
Сравнения преобразований для графических изображений размером 4134x2756 пикселей на базе
вычислений в форматах ПТ и ФТ (рис. 3), показали, что, временя преобразования,
на процессоре Intel Core
2 Duo было уменьшено
более чем в 18-ть (восемнадцать!) раз. Подобное повышение скорости вычислений
является очень значительным и хорошо иллюстрирует эффективность перехода (при
возможности) к формату ФТ даже при наличии математического сопроцессора. Сопоставление
и анализ конечных результатов преобразований с применением ФТ и ПТ показал их
полную идентичность друг другу.
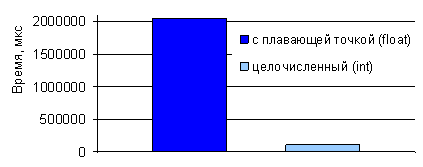
Рис. 3. Сравнение скорости вычислений преобразования
цветовых пространств для
изображения размером 4134x2756
Для полноты рассмотрения вопроса приведём листинг обратного
преобразования из цветового пространства Y709CbCr в RGB в
соответствии с выражением (6) листинг 4.
Листинг 4. Преобразование значения из цветового пространства Y709CbCr в RGB, вычисления производятся в формате ФТ.
ColorSpace x; // пиксель типа ColorSpace
int Y, Cb, Cr;
Y=(int)x.byteLo;
Cb=(int)x.byteAv;
Cr=(int)x.byteHi;
const int
h=((2<<20)>>1); // h=524288;
// компонент (R)
x.byteLo=(uchar)(abs(1220689*Y-1152*Cb+1879436*Cr-259951428+h))>>20;
// компонент (G)
x.byteAv=(uchar)(abs(1220689*Y-223447*Cb-560263*Cr+80783763+h))>>20;
// компонент (B)
x.byteHi=(uchar)(abs(1220689*Y+2216249*Cb+1035*Cr-303343600+h))>>20;
Теперь рассмотрим программу выделения памяти для поля цифрового
сигнала (листинг 5). В качестве примера возьмём статическое изображение с
количеством оттенков 16777215 (0xFFFFFF), для сохранения элементов изображения
будем использовать ранее созданную структуру ColorSpace
(листинг 1).
Листинг 5. Выделение памяти для полноцветного изображения (C++)
// выделяем память
#pragma pack (push, 1)
// объявляем указатель на двумерный массив изображения
ColorSpace** data=0;
// iHeight - высота изображения (число строк)
// iWidth - ширина
изображения (длина строк (столбцы))
data=new
ColorSpace*[iHeight];
for (int i=0; i<iHeight;
i++) {
data[i]=new ColorSpace[iWidth];
memset(data[i], 0, iWidth*
sizeof(ColorSpace)); // инициализация нулём
}
#pragma pack (pop)
// используем выделенную память
// ...
// чистим память
for (int i=0;
i<iHeight; i++)
delete[]data[i];
delete[]data;
data=0;
Отметим, что дефрагментация, возникающая при многократном выделении
памяти, может препятствовать её эффективному использованию и снижению
быстродействия. Существуют так называемые механизмы сборки мусора, позволяющие
своевременно освобождать память.
Способ организации использования выделенного адресного пространства
может существенно повлиять на эффективность вычислений [5,
13-15].
В (листинге 6) приведён пример различных способов перебора двумерного массива.
Результаты работы программы для массива data размером 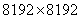 приведены на диаграмме
(рис. 4). Очевидно, что перебор по столбцам, вложенный в перебор по строкам, работает
примерно в два раза быстрее, чем другая пара вложенных циклов. Здесь надо
отметить, что понятия строка и столбец достаточно условны, ведь память ЭВМ
линейна. В соответствии с принятыми названиями (строк и столбцов) и
последовательностью выделения памяти (листинг 5) соседние элементы строки,
расположены по соседним адресам в физической памяти, а элементы столбцов –
удалены друг от друга. Следовательно, при проходе по строке, возможно, более
эффективно использовать преимущества внутрипроцессорной быстродействующей
кэш-памяти, логику предсказания и меньше обращается к более медленной
оперативной памяти [16]. приведены на диаграмме
(рис. 4). Очевидно, что перебор по столбцам, вложенный в перебор по строкам, работает
примерно в два раза быстрее, чем другая пара вложенных циклов. Здесь надо
отметить, что понятия строка и столбец достаточно условны, ведь память ЭВМ
линейна. В соответствии с принятыми названиями (строк и столбцов) и
последовательностью выделения памяти (листинг 5) соседние элементы строки,
расположены по соседним адресам в физической памяти, а элементы столбцов –
удалены друг от друга. Следовательно, при проходе по строке, возможно, более
эффективно использовать преимущества внутрипроцессорной быстродействующей
кэш-памяти, логику предсказания и меньше обращается к более медленной
оперативной памяти [16].
Заметим, что при инициализации возможно многократно быстрее
заполнять фрагменты памяти некоторым константным значением с помощью функций
стандартной библиотеки C
таких как memcpy, memset; при использовании C++, например, инициализацией вектора (std::vector)
при объявлении. В некоторых случаях целесообразно использовать команды
ассемблера для копирования блоков памяти.
Листинг 6. Сравнение способов перебора элементов двумерного массива
(C++).
// заполнение двумерного массива изображения data
// значением содержащимся в temp
UColorSpace temp;
...
// проход по столбцам
for (uint j=0; j<iWidth; j++)
{
// проход по строкам
for (uint i=0; i<iHeight; i++) {
temp.numb=(i+j);
data[i][j]=temp.rgb;
}
}
...
// проход по
строкам
for (uint i=0;
i<iHeight; i++) {
// проход по столбцам
for (uint j=0; j<iWidth; j++) {
temp.numb=(i+j);
data[i][j]=temp.rgb;
}
}
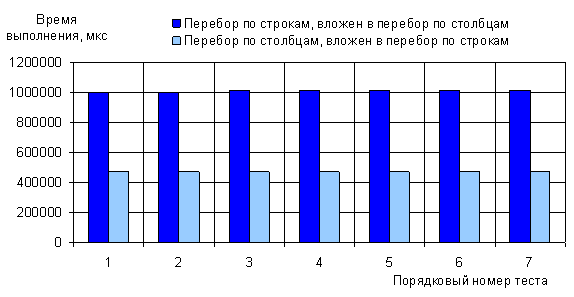
Рис. 4. Время выполнения теста:
способ перебора элементов двумерного массива
Оптимизация программы с точки зрения использования памяти и с
учётом архитектуры конкретной ЭВМ, может существенно повысить скорость
обработки данных.
Заключение
В статье сделан анализ принципов вычислительной оптимизации с применением
арифметики с фиксированной точкой. Рассмотрен принцип практической реализации
на примере взаимного преобразования цветовых пространств RGB в Y709CbCr. При применении
фиксированной точки время вычислений для изображения 4134x2756 на процессоре Intel Core 2 Duo время вычислений сократилось в 18-ть
раз. Такое повышение производительности является очень значимым. Не составляет
труда применить указанный подход к прочим подобным вычислениям, особенно на
современных 64-х и 128-ми разрядных процессорах, когда необходимые значения
умещаются в один процессорный регистр. Сделан анализ способов перебора массива
изображения, показано, что оптимальным
является перебор по столбцам, вложенный в перебор по строкам.
References
1. ITU-R Recommendation BT.601-7 ot 03/2011, Studio encoding parameters of digital television for standard 4:3 and wide-screen 16:9 aspect ratios. ITU, Geneva, Switzerland, 2011.
2. ITU-R Recommendation BT.709, Basic Parameter Values for the HDTV Standard for the Studio and International Programme Exchange [formerly CCIR Rec.709] ITU, Geneva, Switzerland, 2002.
3. Malvar H. S., Sullivan G. J. Transform, Scaling & Color Space Impact of Professional Extensions, ISO/IEC JTC/SC29/WG11 and ITU-T SG16 Q.6 Document JVT-H031, Geneva, May 2003.
4. Gerber R., Bik A., Smit K., Tian K. Optimizatsiya PO. Sbornik retseptov. – SPb.: Piter, 2010. – 325 s.: il
5. Kasperskii K. Tekhnika optimizatsii programm (+CD). S-Pb. Iz-vo: BKhV-Peterburg, 2003 g. – 464 s.:il.
6. Korobeinikov A.G., Kudrin P.A., Sidorkina I.G. Algoritm raspoznavaniya trekhmernykh izobrazhenii s vysokoi detalizatsiei//Vestnik Povolzhskogo gosudarstvennogo tekhnologicheskogo universiteta. Seriya: Radiotekhnicheskie i infokommunikatsionnye sistemy. 2010. № 2. S. 91-98.
7. Grishentsev A.Yu., Korobeinikov A.G. Metody i modeli tsifrovoi obrabotki izobrazhenii. – SPb. : Izd.-vo Politekhn. un-ta, 2014. – 190 s.
8. Grishentsev A.Yu., Korobeinikov A.G. Ponizhenie razmernosti prostranstva pri korrelyatsii i svertke tsifrovykh signalov//Izvestiya vysshikh uchebnykh zavedenii. Priborostroenie. 2016. T. 59. № 3. S. 211-218.
9. Korobeinikov A.G., Aleksanin S.A. Metody avtomatizirovannoi obrabotki izobrazhenii pri reshenii zadachi magnitnoi defektoskopii//Kibernetika i programmirovanie. 2015. № 4. S. 49-61.
10. Korobeinikov A.G., Fedosovskii M.E., Aleksanin S.A. Razrabotka avtomatizirovannoi protsedury dlya resheniya zadachi vosstanovleniya smazannykh tsifrovykh izobrazhenii//Kibernetika i programmirovanie. 2016. № 1. S. 270-291.
11. Grishentsev A. Yu., Korobeinikov A. G. Dekompozitsiya n-mernykh tsifrovykh signalov po bazisu pryamougol'nykh vspleskov. Nauchno-tekhnicheskii vestnik informatsionnykh tekhnologii, mekhaniki i optiki, 2012, № 4 (80).–S. 75-79
12. Grishentsev A. Yu. Effektivnoe szhatie izobrazhenii na baze differentsial'nogo analiza. Rossiiskaya akademiya nauk «Zhurnal radioelektroniki» http://jre.cplire.ru/jre/nov12/index.html, [elektronnyi resurs]// elektronnyi zhurnal, ISSN 1684-1719, №11-noyabr' 2012 g.
13. Grishentsev A. Yu. Sposob szhatiya izobrazheniya. // Patent № 2500067, zayavka № 2012107969/08, prioritet izobreteniya 01.03.2012, zaregistrirovano v Gosudarstvennom reestre izobretenii RF 27.11.2013.
14. Grishentsev A. Yu., Korobeinikov A. G. Postanovka zadachi optimizatsii raspredelennykh vychislitel'nykh sistem // Programmnye sistemy i vychislitel'nye metody. — 2013.-№ 4.-S.370-375.
15. Grishentsev A.Yu. Modelirovanie raspredeleniya plotnosti toka v slozhnom neodnorodnom provodnike. Chast' 1 // Nauchno-tekhnicheskii vestnik informatsionnykh tekhnologii, mekhaniki i optiki. 2006. № 29. S. 87-94.
16. Brei B. Mikroprotsessory Intel: 8086/8088, 80186/80188, 80286, 80386, 80486, Pentium, Pentium Pro, Pentium II, Pentium III, Pentium IV. Arkhitektura, programmirovanie, interfeisy. Shestoe izdanie: Per. s angl. – SPb.: BKhV-Peterburg, 2005. – 1328 s.: il.
Link to this article
You can simply select and copy link from below text field.
|





