MAIN PAGE
> Back to contents
Cybernetics and programming
Reference:
Borodin A.V., Biryukov E.S.
The practical implementation of some algorithms related to the problem of number composing
// Cybernetics and programming.
2015. № 1.
P. 27-45.
DOI: 10.7256/2306-4196.2015.1.13734 URL: https://en.nbpublish.com/library_read_article.php?id=13734
The practical implementation of some algorithms related to the problem of number composing
Borodin Andrey Viktorovich
PhD in Economics
Professor, Department of Computer Science and System Programming, Volga State University of Technology
424000, Russia, respublika Marii El, g. Ioshkar-Ola, pl. Lenina, 3

|
bor@mari-el.com
|
|
 |
Other publications by this author
|
|
|
Biryukov Evgeniy Sergeevich
student, Department of Informatics and System Programming, Volga State University of Technology
424000, Rossiya, respublika Mariy El, g. Yoshkar-Ola, pl. Lenina, 3

|
Eugene.Biryukov@icloud.com
|
|
 |
|
DOI: 10.7256/2306-4196.2015.1.13734
Received:
19-11-2014
Published:
20-01-2015
Abstract:
Among combinatorial algorithms of additive number theory the algorithms of the algorithms for listing compositions of natural numbers have a special place. On the one hand, ideologically, they are among the simplest algorithms in mentioned theory. On the other hand, they play a huge role in all applications somehow connected with the polynomial theorem. In recent years, due to the rapid development of the general theory of risk ideas underlying the polynomial theorem were involved to in the challenges of risk measurement in homogeneous systems of high dimensionality. Solving these problems requires providing mass listing compositions numbers of fixed length and calculating the amount of such compositions for sufficiently large values of both number and the length of composition. In these circumstances, the most urgent task is in effective implementation of these algorithms. The presented article is devoted to the questions related with the synthesis of efficient algorithms for listing the compositions of fixed length and calculating the amount of such compositions. As a methodological base of this study authors use certain facts of set theory, approaches of theory of complex algorithms, as well as some basic results of the theory of numbers. Within this paper, the author propose a new efficient implementation of two algorithms: algorithm for listing all the compositions of fixed length based on the idea of multiset representation of the number partitions and algorithm for calculating the amounts of the compositions of given kind, implemented without involvement of high bitness machine arithmetic. The article shows not only an estimate of the complexity of the proposed algorithms but also presents the results of numerical experiments demonstrating the effectiveness of the implementation of the algorithms discussed in the VBA programming language.
Keywords:
number composition, number expansion, partition of the number, polynomial theorem, multiset, complexity of the algorithm, risk, risk theory, risk measurement, total cost of ownership
This article written in Russian. You can find original text of the article here
.
Введение Пусть `n` – натуральное число. Рассмотрим задачу порождения такого множества целых неотрицательных чисел `{ r_1, quad r_2, quadldots quad, quadr_m }` , что `sum_{k=1}^m quad r_k = n`. В зависимости от ограничений, накладываемых на числа `r_k`, `k=1, quad 2, quad ldots quad, quad m `, постановка этой задачи может несколько видоизменяться. Если порядок чисел `r_k `, `k=1, quad 2, quad ldots quad, quad m `, важен, то последовательность `( r_1, quad r_2, quad ldots quad, quad r_m )` называется композицией или разложением `n `, а число `m` – длиной композиции [5, 7]. При этом обычно накладываются следующие дополнительные ограничения: `r_k > 0 `, `k=1, quad 2, quad ldots quad, quad m `. В отдельных случаях число `m` фиксируется, и тогда возможно рассмотрение композиций, содержащих нулевые элементы, `r_k >= 0 `, `k=1, quad 2, quad ldots quad, quadm `. Эти композиции называются композициями числа `n` из `m` частей. Если порядок `r_k` не важен и `r_k > 0 `, `k=1, quad 2, quad ldots quad, quad m `, то `{ r_1, quad r_2, quad ldots quad, quad r_m }` является мультимножеством и называется разбиением числа `n` [7].
Задача перечисления всех композиций фиксированной длины чрезвычайно тесно связана с полиномиальной теоремой [4]. При этом последняя занимает центральное место в ряде приложений современной теории риска [8].
Такими приложениями являются:
1) оценка риска однородных финансовых инструментов [13], в том числе розничных кредитных портфелей [11];
2) расчет случайной величины совокупной стоимости владения технической системой за период времени при известной дневной статистике отказов [3];
3) расчет случайной величины совокупной стоимости владения технической системой за период времени при имеющихся оценках вероятностей успеха реализации атак злоумышленником в течение некоторого интервала (кванта) времени [9, 12];
4) оценка эффективности системы массового обслуживания клиентов в условиях риска ошибок и злоупотреблений со стороны персонала, а также задачи управления такими системами [1, 2].
Перечень приложений, в которых оценка того или иного вида риска использует результаты полиномиальной теоремы, постоянно расширяется. Во многих таких приложениях приходится массово решать задачи как перечисления композиций числа `n` из `m` частей, так и вычисления количества таких композиций. При этом числа `m` и `n` могут быть достаточно большими. Все это делает разработку эффективных реализаций алгоритмов перечисления композиций фиксированной длины и оценки количества таких композиций чрезвычайно актуальной проблемой.
Задача перечисления композиций фиксированной длины Простейший алгоритм перечисления всех композиций числа `n` фиксированной длины `m` может быть построен на основе того факта, что все эти композиции содержатся в множестве всех возможных образов некоторого упорядоченного множества `A` , мощности `m` , в кольце вычетов по модулю `n+1` :
`forall A quad ( | A | = m ) quad [ { ( r_1, quad r_2, quad ldots quad, quad r_m) } sub { ( f(A)) quad : quad fin Map(A, quadmathbb{Z}_{n+1}}] ` ,
где `( f(A) )` – упорядоченное множество образов элементов множества `A` под действием `f` , это множество упорядочено в порядке следования элементов множества `A` ;
`Map(A, quad mathbb{Z}_{n+1}) = ( mathbb{Z}_{n+1} ) ^ A` – множество всех отображений из `A` в `mathbb{Z}_{n+1}` ;
`mathbb{Z}_{n+1} = {0, quad 1, quad ldots quad, quad n}` – кольцо вычетов по модулю `n+1` .
Сформулируем окончательный принцип формирования композиций фиксированной длины:
`forall A quad ( | A | = m ) quad [ { (r_1, quad r_2, quad ldots quad, quad r_m) } = { (f(A)) quad : quad f in Map(A, mathbb{Z}_{n+1}), quad sum_{x in A} f(x) = n} ]` .
Листинг 1 представляет практическую реализацию этого принципа на языке программирования VBA. Идея построения вариантов упорядоченного множества образов элементов множества `A` под действием отображения `f` заключается в интерпретации образа множества как представления порядкового номера варианта отображения в виде последовательности цифр в системе счисления с основанием `n+1` .
Листинг 1

Для оценки временной сложности предложенного алгоритма используем подход, основанный на оценке временной стоимости каждого оператора языка программирования и подсчете количеств исполнений каждого оператора [6]. Временную стоимость каждой операции примем за 1, а стоимость связки операторов "For i=j to k" и "Next i" оценим как `1 + ( k - j + 1) xx ( 3 + y )` , где `y` – временная стоимость тела цикла.
В результате для функции временной сложности алгоритма имеем:
`f(n, m)=3+1+ (n+1)^m xx quad (3+1+1+m xx (3+2+2)+1+1+m xx (3+1)+1+{[x+1],["0"]}) +1 =`
`=(n+1)^m xx quad (11 m + {[x+9],["8"]} ) + 5` ,
где `x` – временная стоимость процедуры утилизации композиции UtilSplit,
`{[a],[b]}` – возможный выбор из двух альтернатив `a` или `b` .
Таким образом, оценкой сложности [14] предложенного алгоритма является
`Theta ( m(n+1)^m )`. (1)
Алгоритм с такой оценкой сложности вряд ли можно считать приемлимым, по крайней мере в рамках решения задач оценки риска однородных финансовых инструментов [8]. В связи с чем попробуем построить более эффективный алгоритм.
Воспользуемся идеей, положенной в основу доказательства того факта, что общее количество композиций числа `n` длины `m` равно `([n+m-1], [m-1]) = ([n+m-1], [n])` ` ` , где `([n], [m])` – число сочетаний (биномиальный коэффициент) из `n` по `m quad`[7].
Идея заключается в представлении числа `k` мультимножеством `k` единиц. В таком случае композицию числа `n` длины `m` удобно представить в виде упорядоченного мультимножества (массива) длины `n+m-1`, где кроме `n` единиц присутствуют `m-1` нулей, выполняющих функцию разделителей упорядоченного мультимножества на `m` частей (мультимножеств), пустых или состоящих из одних единиц. Перечисление всех таких упорядоченных мультимножеств эквивалентно перечислению композиций числа `n` длины `m`.
Эта идея воплощена в алгоритме, представленном на листинге 2 в виде функции, реализованной на языке программирования VBA. За основу реализации был взят фрагмент кода процедуры возведения в степень полинома, описывающего риск, входящей в пакет прикладных программ "МультиМИР" версии 1.0 [8, 11] (речь идет о процедуре RP).
Листинг 2
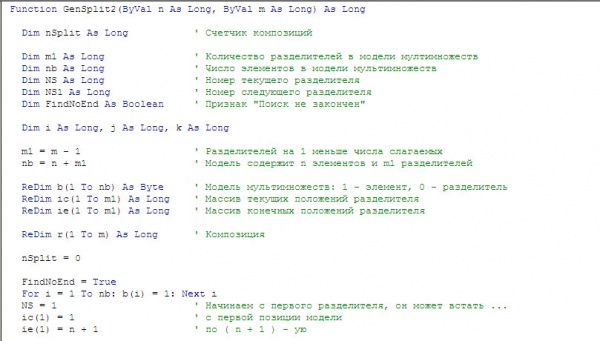
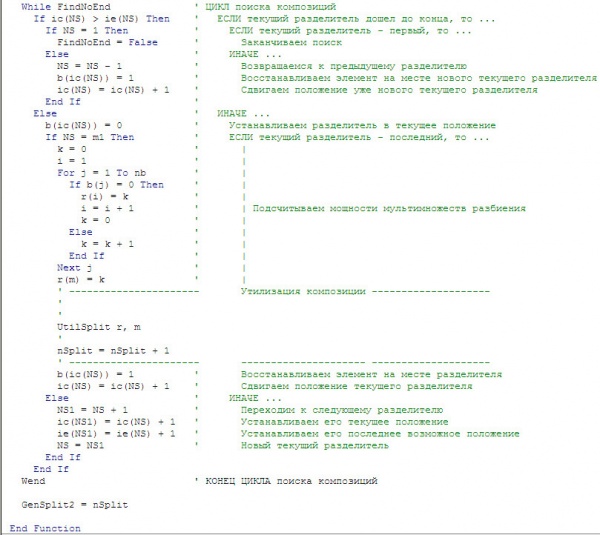
Оценим временную сложность нового алгоритма. Разбор алгоритма позволяет записать:
`f(n, m)=8+1+(n+m-1) xx (3+1) + 3+`
`+C xx ([n+m-1],[n]) xx (1+1+{[1+{["1"],["3"]}],[1+1+{[2+1+(n+m-1) xx (3+1+{["3"],["1"]})+1+x+1+2],["4"]}]})=`
`=4(n+m-1)+12+C xx ([n+m-1], [n]) xx {["4"],["6"],["8"],[{["5"],["7"]} xx (n+m-1) +x +11]}` ,
где `C` – константа, учитывающая в среднем выбор в цикле "While" ветви формирования разбиения мультимножества наряду с ветвью подсчета мощностей мультимножеств и вызова процедуры утилизации очередной сформированной композиции;
`([n+m-1], [n])` – количество композиций числа `n` длины `m`, иначе - это количество повторений ветви подсчета мощностей мультимножеств и утилизации очередной композиции.
Таким образом, оценкой сложности этого алгоритма является
`Theta((n+m-1)xx([n+m-1], [n]))` . (2)
Для сравнения трудоемкости предложенных алгоритмов на практике был проведен численный эксперимент, результаты которого приведены на рис. 1. (Обе оси на графике представлены в логарифмическом масштабе.)
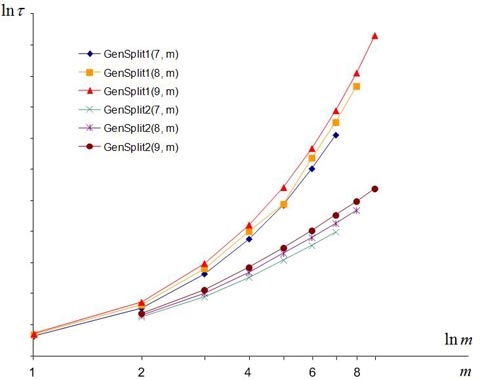
Рис. 1. Результаты численного эксперимента по сравнению временной сложности алгоритмов GenSplit1 и GenSplit2.
Рис. 1 наглядно демонстрирует преимущество второго алгоритма GenSplit2. Однако остается ряд вопросов. Каков характер роста временных затрат алгоритма GenSplit2 с ростом значений параметров? Алгоритм GenSplit2 принципиально лучше алгоритма GenSplit1 или это просто более совершенная реализация того же класса сложности алгоритмов?
Был проведен еще один численный эксперимент по измерению трудоемкости алгоритма GenSplit2 при перечислении композиций натуральных чисел, в разы больших чем в первом эксперименте, см. рис. 2. (Для наглядности на рисунках 1 и 2 использованы одинаковые масштабы осей абсцисс и ординат.)
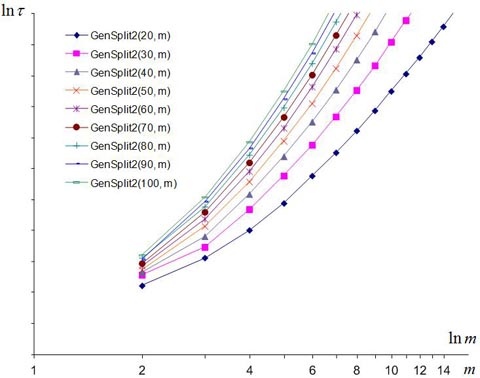
Рис. 2. Результаты численного эксперимента по изучению зависимости временных затрат алгоритма GenSplit2 при перечислении композиций натуральных чисел в диапазоне от 20 до 100 для ряда значений длины композиций.
Сравнивая рисунки 1 и 2, можно выдвинуть гипотезу о совпадении (или существенной близости) классов сложности обоих предложенных алгоритмов. Эта гипотеза находит косвенное подтверждение в монографии [8]. Действительно, в этой работе на стр. 81 приведена иллюстрация, которая показывает, что количество композиций числа `n` длины `m` при `n->oo` асимптотически изменяется как `n^{m-1}` , по крайней мере, если `m/n -> 0` . Иначе говоря, имеет место соотношение
`lim_(n->oo, quad m/n->0) ([n+m-1], [n]) quad = quad c n^{m-1}` , (3)
где `c` – некоторая константа.
Таким образом, оценку (2) с учетом соотношения (3) при условии `m/n-> 0` можно переписать следующим образом:
`Theta((n+m-1)n^{m-1})`. (4)
Хотя обе оценки, (1) и (4), относят оба предложенных алгоритма к классу EXPTIME [14], тем не менее при малых значениях `m` алгоритм с оценкой сложности (4) заметно эффективнее алгоритма с оценкой сложности (1). Это последнее замечание подтверждается в том числе проведенными численными экспериментами.
Задача вычисления количества композиций фиксированной длины Рассмотрим теперь задачу вычисления количества композиций числа `n` длины `m`. Количество таких композиций определяется соотношением [4, 7]:
`([n+m-1], [n]) = {(n+m-1)(n+m-2) quad ldots quad m}/{n!}` . (5)
Реализация "в лоб" алгоритма вычисления количества композиций по формуле (5) на языке программирования VBA приведена на листинге 3.
Листинг 3
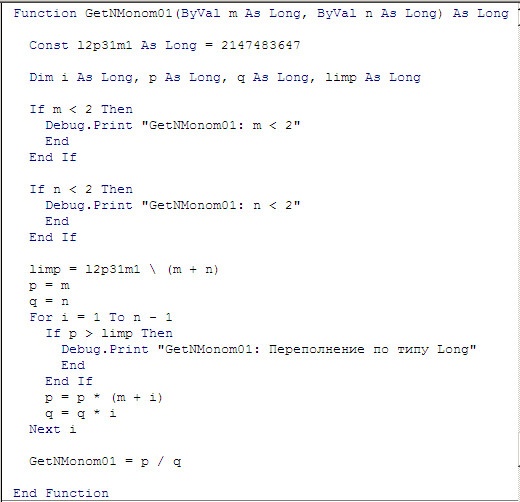
Этот алгоритм содержит элементы контроля возникновения переполнения при перемножении величин типа Long. Тестирование алгоритма показывает, что он останавливается по переполнению даже при не очень больших значениях аргументов `n` и `m`, задолго до того как будут задействованы старшие 2 байта возвращаемого функцией GetNMonom01 значения. Таким образом, эту реализацию алгоритма вычисления количества композиций следует считать неприемлимой.
Простейшим выходом из сложившейся ситуации может быть модификация алгоритма в части деления накопленного числителя на очередной множитель знаменателя при накоплении соответствующих произведений (числителя и знаменателя), в случае, если возможно такое деление нацело. Реализация модифицированного алгоритма приведена на листинге 4.
Листинг 4

Данная модификация алгоритма позволяет отодвинуть границы применимости алгоритма вычисления количества композиций в сторону несколько больших значений параметров `n` и `m`, но этого все еще не достаточно для потребностей практики.
Прежде чем построить новую вычислительную схему, оптимизирующую вычисление правой части соотношения (5), введем ряд обозначений. Пусть `vec p` – вектор, компонентами которого являются первые `l` простых чисел:
`vec p = (p_i)_{i=1}^{l} quad = (2, quad 3, quad 5, quad 7, quad 11, quad ldots quad), quad p_i in mathbb P, quad i=1, quad 2, quad ldots quad, quad l,`
здесь `mathbb P` – множество простых чисел.
Пусть, далее, `vec f` – вектор-функция частичной факторизации:
`(e_i)_{i=1}^l quad = vec {f} (vec p, n) quad hArr_{Def} quad n = mprod_{i=1}^l p_i^{e_i}, `
`e_i in ZZ_0^{+}, quad m != 0 (mod quad p_i), quad i=1, quad 2, quad ldots quad, quad l,`
`g` – функция, возвращающая остаточный член, возникающий при частичной факторизации:
`m=g(vec p, n) quad hArr_{Def} quad n = m prod_{i=1}^l p_i^{e_i},`
`e_i in ZZ_0^{+}, quad m!=0(mod quad p_i), quad i=1, quad 2, quad ldots quad, quad l,`
где `ZZ_0^{+}` – множество неотрицательных целых чисел.
И, наконец, пусть `pi` – функция, формирующая число из результатов его частичной факторизации:
`pi(vec p, quad vec e, quad m) =_{Def} m prod_{i=1}^l p_i^{e_i}.`
Пользуясь введенными обозначениями, соотношение (5) можно переписать следующим образом:
`([n+m-1], [n]) = pi (vec p, quad sum_(i=0)^{n-1} vec{f}(vec p, quad m+i) - sum_(i=1)^n vec{f}(vec p, quad i), quad {prod_(i=0)^{n-1} g(vec p, quad m+i)}/{prod_(i=1)^n g(vec p, quad i)}) . (6)`
На основе соотношения (6) можно построить новый алгоритм вычисления количества разбиений. Так на листинге 5 представлена часть реализации этого алгоритма, связанная с описанием структур данных и инициализации массива простых чискл. Реализация самого алгоритма приведена на листинге 6.
Листинг 5
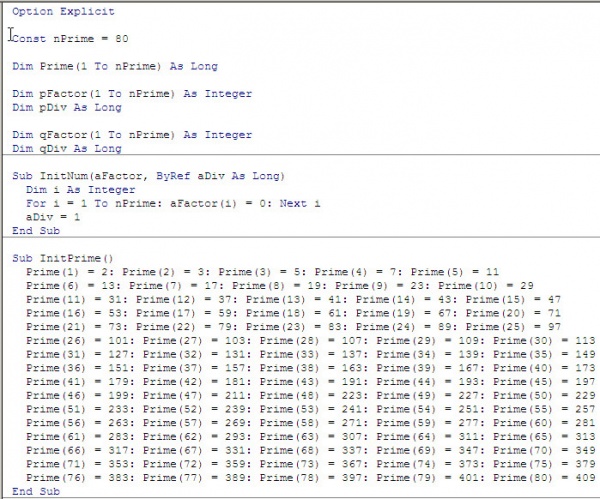
Листинг 6

На листинге 7 приведен код вспомогательных процедур, используемых основным алгоритмом.
Листинг 7
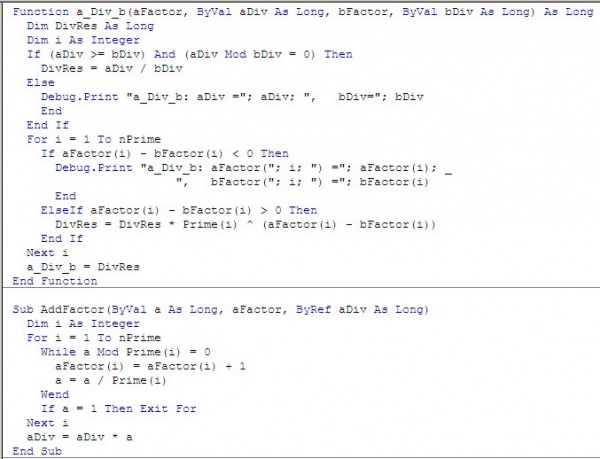
Тестирование функции GetNMonom2 продемонстрировало ее способность вычислять количества композиций, исчисляющиеся величинами в пределах числа `2^31 - 1` .
Заключение Основным результатом данной работы является выбор двух алгоритмов для практического использования в приложениях, так или иначе использующих полиномиальную теорему. Это алгоритм перечисления композиций фиксированной длины и алгоритм расчета количества таких композиций. Первый из этих алгоритмов отличается заметно более высокой производительностью среди исследованных. Второй алгоритм реализует вычисление количества композиций числа фиксированной длины без привлечения арифметики высокой разрядности и без ограничений на значения аргументов в пределах используемых типов для входных и выходных параметров алгоритма.
Частным результатом работы можно считать наглядную демонстрацию производительности конкретных реализаций алгоритмов перечисления композиций. Эту информацию могут использовать специалисты для оценки потребности в вычислительных ресурсах для моделей, использующих описанные в работе алгоритмы.
Дальнейшим развитием исследований, описанных в данной статье, представляется работа по совершенствованию алгоритма, реализованного в рамках функции GenSplit2, в направлении снижения коэффициента перед выражением `(n+m-1)([n+m-1], [n])` в функции временной трудоемкости алгоритма.
References
1. Borodin, A. V. Arkhitektura informatsionnoi sistemy podderzhki prinyatiya reshenii po upravleniyu personalom roznichnoi podsistemy kommercheskogo banka // Programmnye sistemy i vychislitel'nye metody. – 2014. – №2. – S. 174–190. – DOI: 10.7256/2305–6061.2014.2.12331.
2. Borodin, A. V. Modeli upravleniya personalom v roznichnoi podsisteme kommercheskogo banka / A. V. Borodin // Ekonomika i sotsium: sovremennye modeli razvitiya obshchestva v aspekte globalizatsii: materialy III mezhdunarodnoi nauchno-prakticheskoi konferentsii (12 fevralya 2014 g.). – Saratov: Izdatel'stvo TsPM «Akademiya Biznesa», 2014. – S. 26–30.
3. Borodin, A. V. Stokhasticheskoe modelirovanie v zadachakh sinteza optimal'nykh topologii setei distributsii tochnogo vremeni / A. V. Borodin, D. R. Zub'yak // Tekhnicheskie nauki – ot teorii k praktike. Sbornik statei po materialam XXXIV mezhdunarodnoi nauchno-prakticheskoi konferentsii. № 5 (30). – Novosibirsk: Izdatel'stvo «SibAK», 2014. – S. 7–15.
4. Vilenkin, N. Ya. Kombinatorika / N. Ya. Vilenkin. – M.: Nauka, 1969. – 328 s.
5. Kompozitsiya chisla // Vikipediya. Svobodnaya entsiklopediya. – URL: https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D1%8F_%D1%87%D0%B8%D1%81%D0%BB%D0%B0. Data obrashcheniya: 17.11.2014.
6. Kormen, T. Kh. Algoritmy: postroenie i analiz / T. Kh. Kormen, Ch. I. Leizerson, R. L. Rivest, K. Shtain. – M.: OOO «I. D. Vil'yams», 2013. – 1328 s.
7. Reingol'd, E. Kombinatornye algoritmy: teoriya i praktika / E. Reingol'd, Yu. Nivergel't, N. Deo. – M.: Mir, 1980. – 477 s.
8. Urazaeva, T. A. Algebra riskov / T. A. Urazaeva. – Ioshkar-Ola: Povolzhskii gosudarstvennyi tekhnologicheskii universitet, 2013. – 209 s.
9. Urazaeva, T. A. Instrumental'nye metody analiza riska v ekonomike bezopasnosti vychislitel'nykh setei / T. A. Urazaeva // Materialy III Mezhdunarodnoi nauchno-prakticheskoi konferentsii «Innovatsionnoe razvitie rossiiskoi ekonomiki». Chast' 1. – M.: MESI, 2010. – S. 246-250.
10. Urazaeva, T. A. Paket prikladnykh programm «Mul'tiMIR»: arkhitektura i primenenie / T. A. Urazaeva // NB: Kibernetika i programmirovanie. – 2014. – № 5. – S.34-61. – DOI: 10.7256/2306-4196.2014.5.12962. – URL: http://e-notabene.ru/kp/article_12962.html.
11. Urazaeva, T. A. Paket prikladnykh programm «Mul'tiMIR» v praktike analiza kreditnogo riska / T. A. Urazaeva // VIII Mezhdunarodnaya nauchno-metodicheskaya konferentsiya «Sovershenstvovanie podgotovki IT-spetsialistov po napravleniyu «Prikladnaya informatika» dlya innovatsionnoi ekonomiki»: Sbornik nauchnykh trudov. – M.: Moskovskii gosudarstvennyi universitet ekonomiki, statistiki i informatiki, 2012. – S. 182-186.
12. Urazaeva, T. A. Stoimostnoi analiz riska narusheniya odnoi politiki bezopasnosti v vychislitel'nykh setyakh / T. A. Urazaeva // Modelirovanie i analiz bezopasnosti i riska v slozhnykh sistemakh: Trudy Mezhdunarodnoi nauchnoi shkoly MA BR – 2010 (Sankt-Peterburg, 6-10 iyulya, 2010 g.). – SPb.: GUAP, SPb., 2010. – S. 193-199.
13. Urazaeva, T. A. Finansovye riski: algebraicheskaya model' ischisleniya / T. A. Urazaeva // Regional'naya ekonomika: teoriya i praktika. – 2010. – № 2(137). – S. 33-35.
14. Arora, S. Computational Complexity: A Modern Approach / S. Arora, B. Barak. – New York: Cambridge University Press, 2009. – 594 p.
Link to this article
You can simply select and copy link from below text field.
|





