Developing of the mathematical and simulation models for calculation of an estimate of informatization object protection from unauthorized physical access

Korobeinikov Anatolii Grigor'evich Doctor of Technical Science professor, Pushkov institute of terrestrial magnetism, ionosphere and radio wave propagation of the Russian Academy of Sciences St.-Petersburg Filial 199034, Russia, g. Saint Petersburg, ul. Mendeleevskaya, 1 Korobeynikov_A_G@mail.ru Other publications by this author     Grishentsev Aleksei Yur'evich Doctor of Technical Science Associate Professor, St. Petersburg National Research University of Information Technologies, Mechanics and Optics 197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49 grishentcev@ya.ru Other publications by this author     Kutuzov Il'ya Mikhailovich graduate student, Department of Design and Security of Computer Systems, St. Petersburg National Research University of Information Technologies, Mechanics and Optics 197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49 formalizator@gmail.com Other publications by this author     Pirozhnikova Ol'ga Igorevna graduate student, Department of Design and Security of Computer Systems, St. Petersburg National Research University of Information Technologies, Mechanics and Optics 197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49 cheezecake@mail.ru Other publications by this author     Sokolov Kirill Olegovich graduate student, Department of Design and Security of Computer Systems, St. Petersburg National Research University of Information Technologies, Mechanics and Optics 197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49 Korobeynikov_A_G@mail.ru

Litvinov Dmitrii Yur'evich graduate student, Department of Design and Security of Computer Systems, St. Petersburg National Research University of Information Technologies, Mechanics and Optics 197101, Russia, St. Petersburg, Kronverkskiy prospect, d. 49 litvinovdiman92@mail.ru

Проведенный анализ текущего состояния разработки методов и средств одной из важнейшей компоненты комплексной системы информационной безопасности (КСИБ), а именно системы охранной сигнализации (СОС), показал, что для того, что бы СОС соответствовали основным требованиям к современной защите объектов информатизации (ОИ), то эти системы необходимо постоянно развивать. А ввиду того, что в настоящее время происходит интенсивное внедрение КСИБ во многие организации различной формы собственности, следует, что разработка различных математических и имитационных моделей для расчета оценки защищенности ОИ от несанкционированного физического проникновения (НФП) является актуальной задачей.

При решении вышеназванной задачи в предлагаемой работе были использованы: методы защиты информации, методы теории графов и теории вероятности. Реализация результатов в программное обеспечение было проведено при помощи системы компьютерной алгебры Maple ^[1].

Представляемая методика расчета оценки защищенности ОИ от НФП базируется на:

– математической модели (ММ) для расчета вероятности НФП на ОИ:

– имитационной модели (ИМ) для расчета оценки защищенности ОИ от НФП.

Рассмотрим первую составляющую. Разработка ММ для расчета вероятности НФП на ОИ (далее просто ММ) была представлена в ^[2]. Рассмотрим построение ММ на достаточно произвольном примере.

Используя методы теории графов, строим ММ в виде ациклического графа G. Задав все вершины и ребра G, определяем матрицу смежности, показывающей связь между ij – ым и kl – ым местом (под местом понимается комната, лестница, коридор и т.д.). Схематически маршрут в G можно представить в виде, изображенном на Рис. 1. Далее, задаем вершину (место) j_d, куда стремится попасть злоумышленник. Затем происходит вычисление всех потенциально опасных маршрутов из заданного набора вершин(мест) в вершину j_d.

Для примера рассмотрим ОИ с четырьмя этажами и пятью местами на каждом этаже. Примерное расположение выглядит следующим образом.

Место № 1 – улица.

Первый этаж: 2,5 – служебные помещения, 3 – коридор, 4 – проходная, 6 – лестница.

Второй этаж: 7,8,10 – служебные помещения, 9 – коридор, 11 – лестница.

Третий этаж: 12,13,14 – служебные помещения, 15 – коридор, 16 – лестница.

Четвертый этаж: 17,18,19 – служебные помещения, 20 – коридор, 21 – лестница.

Место (помещение) куда хочет проникнуть злоумышленник – j_d = 14.

Зададим веса (длина пути из i-го места в j – ое) ребер.

На языке Maple это выглядит следующим образом:

p:=1·10e20; # Очень большое число

E:={[[1,2], 800], [[1,3], 800], [[1,4], 4], [[1,5], 800], [[1,6], 800], [[1,7], 1500], [[1,8], 1500], [[1,9], 1500], [[1, 10], 1500], [[1, 11], 1500], [[1, 12], 300], [[1, 13], 3000], [[1, 14], 3000], [[1, 15], 3000], [[1, 16], 3000], [[1,17], 4000], [ [ 1, 18], 4000], [ [ 1, 19], 4000], [ [ 1,20], 4000], [[1,21], 4000], [[2,3], 2], [[2,4], 250], [ [2, 5],р], [ [2,6], р], [[2,7], 400], [[2,8],р], [ [2,9 ],р], [ [2,10],р], [ [2,11], р], [ [2,12],р], [ [2,13],р], [ [2,14],р], [ [2,15 ],р], [ [2, 16],р], [[2,17],р], [[2,18],р],[[2,19],р],[[2,20],р], [[2,21],р],[[3,4],2], [[3,5],2], [[3,6],1], [[3,7],р],[[3,8],р],[[3,9],500],[[3,10],р],[[3,11],р],[[3,12],р],[[3,13],р], [[3,14],р],[[3,15],р],[[3,16],р],[[3,17],р],[[3,18],р],[[3,19],р],[[3,20],р],[[3,21],р],[[4,5],400],[[4,6],р],[[4,1],р],[[4,8],500],[[4,9],р],[[4,10],р], [[4,11],р],[[4,12],р],[[4,13],р],[[4,14],р],[[4,15],р],[[4,16],р],[[4,17],р],[[4,18],p],[[4,19],р],[[4,20],р],[[4,21],р],[[5,6],400],[[5,7],p],[[5,8],р], [[5,9],р],[[5,10],500],[[5,11],р],[[5,12],р],[[5,13],р],[[5,14],р],[[5,15],р],[[5,16],р],[[5,17],р],[[5,18],р],[[5,19],р],[[5,20],р],[[5,21],р],[[6,7],р],[[6,8],р],[[6,9],р],[[6,10],р],[[6,11],2],[[6,12],р],[[6,13],р],[[6,14],р],[[6,15],р],[[6,16],р],[[6,17],р],[[6,18],р],[[6,19],р],[[6,20],р],[[6,21],р], [[7, 8], 300], [[7,9],4],[[7,10],р],[[7,11],р],[[7,12],500],[[7,13],р], ^[7,14],р],[[7,15],р],[[7,16],р],[[7,17],р],[[7,18],р],[[7,19],р], [[7,20],р],[[7,21],р],[[8,9],4],[[8,10],400],[[8,11],р],[[8,12],р],[[8,13],500],[[8,14],р],[[8,15],p],[[8,16],p],[[8,17],р],[[8,18],p],[[8,19],р],[[8,20],p],[[8,21],р],[[9,10],4],[[9,11],2],[[9,12],р],[[9,13],р],[[9,14],р], [[9,15],500],[[9,16],р],[[9,17],p],[[9,18],р],[[9,19],р],[[9,20],р],[[9,21 ],р], [ [10,11 ], 400], [ [ 10,12],р],[[10,13],р],[[10,14],500],[[10,15],р], [[10,16],р], [[10,17],р], [[10,18],р],[[10,19],р],[[10,20],р], [[10,21],р], [[11,12],р],[[11,13],р],[[11,14],р],[[11,15],р],[[11,16],2],[[11,17],р], [[11,18],р],[[11,19],р],[[11,20],р],[[11,21],р],[[12,13],400],[[12,14],р],[[12,15],2],[[12,16],р],[[12,17],500],[ [12,18],р],[[12,19],р],[[12,20], р],[[12,21],р],[[13,14],400],[[13,15],2],[[13,16],р],[[13,17],р],[[13,18],500], [[13,19],р], [[13,20],р], [[13,21],р],[[14,15],2],[[14,16],400],

[[14,17],p],[[14,18],р],[[14,19],500], [[14,20 ],р],[[14,21],р],[[15,16], 2], [[15,17],р],[[15,18],р],[[15,19],p], [[15,20],500],[[ 15,21 ],р],[[16, 17],р], [[16,18],р],[[16,19],р], [[16,20],р], [[16,21], 2],[[ 17,18 ],400], [[17,19],р],[[17,20],р], [[17,21],р],[[18,19],400],[[18,20],2],[[18,21], р], [[19,20], 2],[[19,21],p], [[20,21], 2]}:

Соответствующий граф представлен на рис. 2.

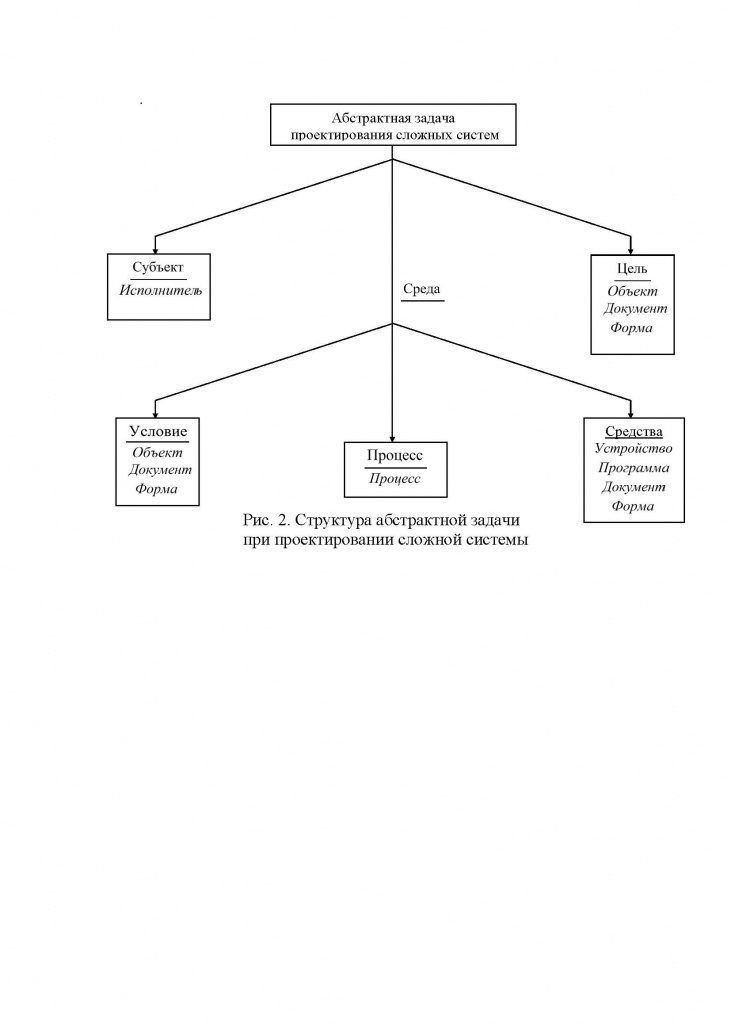
Рис.2. Орграф, соответствующий операторам Maple

Далее, при помощи алгоритма Дейстры, вычисляем наиболее предпочтительные (потенциально опасные) пути и их длину (сумма весов соответствующих ребер) из заданных вершин в вершину j_d ^[1,3,4].

M_{1_14}={(1,4,8,9,10,14),1012}, M_{2_14}={(2,7,9,10,14),908},

M_{3_14}={(3,5,10,14),1002}, M_{4_14}={(4,8,9,10,14),1008},

M_{5_14}={(5,10,14),1000}, M_{6_14}={(6,14), 1·10e20},

M_{7_14}={(7,9,10,14),508}, M_{8_14}={(8,9,10,14),508},

M_{9_14}={(9,10,14),404}, M_{10_14}={(10,14),500},

M_{11_14}={(11,14), 1·10e20}, M_{12_14}={(12,13,14),800},

M_{13_14}={(13,14),800}.

Зададим вектор обнаружения НФП в каждой вершине: ОФП_n=(p₁, p₂,…,p_n), где n – количество вершин в G. Это означает, что установленные в конкретном месте сенсоры обнаруживают НФП с заданной вероятностью. На языке Maple, для рассматриваемо примера, это можно сделать так:

P:=<0.05,0.35,0.45,0.68,0.24,0.28,0.3,0.34,0.23,0.45,0.34,0.5,0,5, 0.55,0.48,0.34,0.43,0.28,0.34,0.32,0.38>

После этого, применяя теорему о сложении вероятностей, рассчитываются вероятности обнаружения физического проникновения на каждом из полученных путей.

Полученные результаты расчета вероятностей обнаружения физического проникновения на каждом из полученных путей представлены в таблице 1.

Таблица 1.

Вероятности обнаружения физического проникновения

Обычно считается, что злоумышленнику известны значения матриц A_смежн и W, а также вектора ОФП_n. Его цель в нахождении возможных путей, на которых его обнаружат с минимальной вероятностью. А вот цель комплексной системы защиты ОИ – сделать эту вероятность максимальной.

Далее строится имитационная модель, позволяющая производить количественную оценку защищенности от НФП на ОИ. Типовая структурная схема представлена на Рис. 3.

Рис. 3. Структурная схема имитационной модели оценки защищенности от НФП на ОИ.

На Рис. 3 приняты следующие обозначения: V_i(t) – входные потоки, U_i. – множество потенциальных угроз, S_i. – набор средств защиты, – поток нераспознанных (пропущенных) системой защиты от НФП, – выходной поток.

Потоки запросов на систему защиты от НФП, поступают по m каналам, разрежаются с вероятностями p_i, зависящими от используемых системой защиты (СЗ) средств обнаружения и блокирования от НФП. К каждому такому средству поставлена вероятность пропуска НФП – q_i. Отсюда следует, что вероятность обеспечения защиты (отражения НФП) равна p_i = 1–q_i.

Факт неполного закрытия системой защиты всех возможных каналов проявления угроз учитывается отсутствием для m-n входных потоков средств защиты, что означает =V_i(t), i = n+1, n+2, ... m.

«Злоумышленник» является начальным блоком модели, в которой предполагается, что он не подвергается входным воздействиям. Основное назначение блока – генерация потока запросов (транзактов) НФП с заданной интенсивностью λ_i, т.е. реализация угроз НФП на ОИ с соответствующими интенсивностями. Формально Злоумышленник характеризуется вектором интенсивностей λ={ λ₁, λ₂, … λ_m} попыток реализации соответствующих угроз U₁…U_m.

Блок «СЗ» имитирует процесс реагирования СЗ на запросы от блока «Злоумышленник». Основной задачей блока СЗ является отсеивание запросов НФП с определенной (заданной) вероятностью, то есть распознать угрозу и заблокировать несанкционированный запрос. На выходе блока образуется выходной поток , являющимся объединением выходных потоков i-средств защиты и потока НФП-запросов, приходящих по m-n неконтролируемым каналам.

Последний блок модели – «Защищаемые ОИ» – уничтожает запросы НФП (транзакты).

Нарушитель в модели представлен рядом генераторов транзактов, каждый из которых имитирует поступление в систему НФП-запросов с соответствующими интенсивностями λ_i. Механизмы защиты СЗ от НФП состоят из трех блоков: очереди (буфера запросов на обслуживание), блока ожидания, имитирующего обработку запроса НФП и условного ветвления, имитирующего результат обработки. Два блока уничтожения транзактов служат для вывода транзактов из модели. Наличие этих блоков в модели является необходимым условием ее работоспособности.

В данной модели суммарный поток НФП рассматривается как Пуассоновский поток. В этом случае интенсивность потока пропущенных запросов НФП вычисляется по формуле:

` H(t)=sum_(n=1)^m lambda_(i)q_(i)t`

Вероятность обеспечения защиты означает вероятность отсутствия случаев НФП на ОИ и поэтому в данной модели вычисление оценки защищенности производится по формуле:`Z(t)=e^(-H(t)) =e^(-sum_(n=1)^m lambda_(i)q_(i)t` (Вероятность того, что за время t не сработал ни один датчик)

Алгоритм работы имитационной модели имеет следующий вид. Генератор транзактов генерирует с заданной интенсивностью запросы НФП. Запросы поступают в очередь. Если i – ый блок обработки свободен, запрос НФП поступает на обслуживание. После этого он с вероятностью p_i отсеивается (поступает в блок “Защищенные ОИ” для уничтожения транзактов) или с вероятностью q_i пропускается в систему (поступает в блок “Незащищенные ОИ” для уничтожения транзактов).

Структурная схема работы имитационной модели представлена на Рис. 4.

Функционирование разработанной имитационной модели продемонстрируем на данных, полученных в вышеприведенном примере. На Рис. 5 представлены результаты имитационного моделирования для получения оценки защищенности наиболее предпочтительного пути с улицы в помещение № 10 для разного количества попыток НФП.

Рис. 5. Оценка защищенности наиболее предпочтительного пути с улицы в помещение № 14 для разного количества угроз НФП.

На Рис. 6 представлены результаты имитационного моделирования для получения оценки защищенности различных путей в помещение № 14 для 5 угроз НФП.

Рис. 6. Оценка защищенности различных путей в помещение № 14 для 5 угроз НФП.

Накопленная в результате имитационного моделирования статистика позволяет определить основные характеристики, необходимые для расчета защищенности ОИ от НФП.

Заключение

Подводя итог, можно сказать, что разработанная имитационная модель позволяет моделировать процесс защиты ОИ от НФП. В обоих выполненных численных экспериментах относительная ошибка, характеризующая расхождение характеристик СЗ, рассчитанных теоретически и полученных в результате имитационного моделирования, составила 0,1%.

You can simply select and copy link from below text field.