|
DOI: 10.7256/2409-8736.2017.1.22616
Received:
07-04-2017
Published:
23-04-2017
Abstract:
The subject of the study is a very important and urgent issue of modern education - the training of competent professionals who are able to make weighted management decisions in various fields of activity.The subject of the study is the role and significance of mathematical culture in enhancing the professional competence of students in economic and related areas of training.Particular attention is paid to the study of the connection between mathematical culture and professional competence. The modern state of mathematical education is described, the relation of mathematics and computer science is analyzed, the use of information and computer technologies in mathematical education is analyzed.The methodology of the study is based on the theory of modeling, based on the formal-constructive interpretation of the model. Methods of research: analysis of own pedagogical practice of mathematical education, analysis and synthesis of advanced Russian and foreign research, modeling.The main findings of the study are:1. The mathematical culture of the graduate and specialist remains one of the key components of the culture of modern society.2. The professional competence of the graduate and specialist includes a cultural component, of which the mathematical culture is an integral part.3. A specially organized mathematical education at the economic university allows successfully to solve the problem of increasing the professional competence of the graduate.The novelty of the research is that at the basis of this special organization is the model of mathematical culture as an infrastructure for the perception and processing of information and the exchange of information consisting of a system of phenomena, a system of relations, a system of interfaces and a management system.
Keywords:
professional competence, culture, mathematical culture, language of mathematics, mathematical models, the mathematization of society, mathematical education, information technologies in education, modeling theory, mathematical culture model
This article written in Russian. You can find original text of the article here
.
В современном обществе проблема принятия
решений на различных уровнях управления является весьма важной и актуальной. Во
многом принятие эффективных решений определяется компетентностью лиц, эти
решения принимающих. Вместе с тем, сложность процессов, происходящих в
обществе, вызывает значительные трудности при выборе той или иной стратегии на
всех уровнях, будь то фирма, корпорация, регион и т.д.
Принятие решений является сложной
системной задачей, требующей адекватных методов, причём все чаще этот процесс опирается
на математические методы. Язык математики является одним из важных компонентов
коммуникации. Если собеседник не понимает смысла фразы «но тогда возрастет
дисперсия таких-то значений» или «зависимость между величинами линейная», то
передача смысла сообщения превращается в утомительный процесс, зачастую с
непредсказуемым результатом. Поэтому необходим соответствующий уровень
математизации общества, иначе говоря, речь идет о математической культуре общества.
Взаимосвязь математической культуры и
юридического образования рассматривается в [1]. В статье [2] на основе
анализа исследований педагогов по вопросу культуры сделан вывод, что культура
удовлетворяет критериям системности. В работе [3] математическая
культура рассматривается как высшее проявление человеческой образованности и
профессиональной компетентности.
Педагогические основы понятия «математическая
культура студентов» рассмотрены в [4]. В работе [5] рассмотрена математическая
культура личности, структура и содержание которой рассматривается в [6], в
которой сделан вывод, что математическая культура общества является родовым
понятием по отношению к математической культуре личности.
Р.Н. Щербаков в [7] ограничился математической культурой
учащегося. Роль математической культуры в становлении и развитии творческого
потенциала современного специалиста рассматривается в [8], а в [9] изучается
математическая культура студентов высших учебных заведений естественнонаучного
и инженерно-технического профилей.
И.Г. Липатникова [10]
рассматривает математическое образование в контексте диалога культур на трех
уровнях: всего человечества, государства, личности. Т.В. Дубынина [11]
изучает математическую культуру как элемент современного образования.
Р.М. Зайниев [12] использовал взгляд на математическую культуру как
на основу подготовки инженера. В [13] математическая культура изучается
как компонент высшего профессионального образования, а в [14] – как аспект
профессиональной культуры.
Интересно, что в известном исследовании
по мультикультурализму [15] рассматривается взаимодействие национальных,
государственных и других естественных культур, но взаимодействие культур
отдельных видов деятельности (в том числе математической) не рассматривается.
Включение математической культуры в состав культуры в целом, «математическая
инкультурация» рассматривается А.Бишопом [16]. Взаимодействие культуры
страны и корпоративной культуры рассматривается в [17].
Один из вариантов трактовки термина «культура» обусловлен результатами анализа
её предназначения [18, С. 175-179]. Этот вариант корректен, поскольку
культура, с одной стороны, является результатом целенаправленной деятельности
и, с другой стороны, обеспечивает целенаправленность деятельности.
Математическая культура как феномен
весьма многообразна, дать её формальное логическое определение невозможно.
Правильнее говорить о различных аспектах, моделях
математической культуры. Мы будем говорить о модели математической культуры выпускника экономического университета. Почему
выделение этого аспекта является важным? Потому что выпускники экономических
вузов в большинстве случаев должны принимать те самые решения, от которых
зависит развитие нашего общества. И качество этих решений должно обеспечиваться
системой образования.
Мы полагаем, что о математической культуре выпускника экономического университета
следует говорить особо. Поясним
сказанное. Известный российский математик и популяризатор науки Владимир
Андреевич Успенский совершенно справедливо говорит о необходимости лоббирования
включения в общеобязательный культурный багаж математической составляющей:
«Включение же в этот багаж чего-то математического в качестве обязательной
составной части многим может показаться непривычным и потому нуждается в
лоббировании» [19, С. 13].
В последние годы в образовании
наметилась тревожная тенденция объединения математики и информатики:
объединение кафедр, объединение учебных курсов. Исторически сложилось так, что
информатика (первоначально входившая в кибернетику) фактически была компонентом
математики. Это было обусловлено исключительной ролью вычислительного аппарата
математики: до второй половины XX века владение
математикой означало умение вычислять, в том числе проводить символьные
вычисления, причём выкладки могли быть очень громоздкими. В настоящий момент
вычислительный аппарат математики в значительной степени интегрирован в
информационные технологии. В различных областях деятельности системы типовых
математических моделей нередко выделяются в относительно самостоятельные
дисциплины: эконометрику, финансовую математику, математическое моделирование
в… и др. Даже среди профессиональных математиков все большую популярность
набирают компьютерные программы символьных вычислений, часть из которых не
является коммерческим продуктом и распространяется в рамках различных свободных
лицензий, например, GAP, Maxima. Таким образом, эпоха абсолютизации вычислительного
аппарата математики завершилась. На этом основании горячие головы предлагают
совсем отказаться от курса математики полностью заменив её интегрированными
курсами или оставив от математики только отдельные фрагменты, включенные в
другие курсы: информатики, экономики и др. Включение математического
материала в эти курсы нередко целесообразно, однако отказ от систематического
изучения математики, формирования цельного представления о математике, её
методах, возможностях и ограничениях, стиле мышления, приведет к катастрофе.
Отсутствие математической культуры приводит к грубым ошибкам в управлении,
моделировании и применении вычислительного аппарата математики, несмотря на
использование самой современной компьютерной техники и программного
обеспечения.
Примеры таких ошибок: применение
смещенных оценок значений случайных величин или бездумное использование средних
значений в качестве оценок без анализа того, насколько эта оценка адекватна используемой
ситуации, суммирование расходящихся
рядов: абсурдное вычисление суммы гармонического ряда с заданной точностью... На
практике нередко наблюдается отождествление математического мышления с
алгоритмическим, что является грубейшей ошибкой.
Таким образом, поднятая нами проблема
сохранения собственно математической культуры является актуальной и значимой. В
первую очередь, это касается математического образования.
Математическую культуру естественно
рассматривать как неотъемлемую часть культуры общечеловеческой. Обсуждение
вопроса о том, что такое культура и какова её роль в жизни общества имеет
давнюю богатую историю. На наш взгляд, сформулировать общепринятое определение
культуры к настоящему моменту не удалось и, видимо, невозможно в силу многогранности
и многоаспектности этого понятия. Но понятие вводится в обиход не только
дедуктивно, с помощью определения, но и индуктивно, с помощью достаточного
числа примеров, моделей этого понятия.
В русской версии Википедии (просмотр от
5 апреля 2017 года) приводятся различные трактовки понятия «культура». Из Большой советской
энциклопедии: «исторически определённый
уровень развития общества и человека, выраженный в типах и формах организации
жизни и деятельности людей, а также в создаваемых ими материальных и духовных
ценностях»; Ю. М. Лотман: «совокупность
генетически ненаследуемой информации в области поведения
человека»; «практическая реализация общечеловеческих
и духовных ценностей» [20]; «вся
совокупность небиологических проявлений человека» [21]; Э.О. Уилсон (более «техническое» описание): «культуру, в том числе наиболее
блистательные и впечатляющие её проявления в виде ритуальных и религиозных
служб, можно интерпретировать как иерархическую систему приспособлений и
устройств для отслеживания параметров среды».
Нам представляется, что теория
моделирования [22] открывает новые возможности в изучении понятия
«культура». Рассмотрим экзоструктурную
модель культуры, т.е. модель, в которой развернуты, раскрыты связи культуры
с «внешними объектами». В частности, рассмотрим предназначение культуры, т.е.
попробуем ответить на вопрос «что выделяет культурного человека?». Мы делаем
соответствующий вывод только на основании реакции субъекта на сообщаемую
информацию: насколько быстро и точно он её воспринимает, какие выводы из неё
делает (насколько эти выводы глубокие, адекватные, неочевидные и т.п.).
Следовательно, математическую культуру (далее мы будем говорить только о ней)
можно понимать как инфраструктуру для восприятия и обработки информации средствами
математики. Таким образом, мы предлагаем модель математической культуры
как инфраструктуры для обработки информации, состоящей из системы
математических феноменов, интерфейсов между ними и механизмов управления. Улучшение
математической культуры означает: а) увеличение числа математических
феноменов, б) увеличение числа интерфейсов, инструментов для связи между
разными математическими феноменами; в) улучшение механизма управления.
Уровень математической культуры определяется, во-первых, обилием математических
феноменов, которыми владеет субъект, во-вторых, обилием интерфейсов между ними
и уровнем владения этими интерфейсами. Эти величины измеримы! Следует изменить
систему контроля, сделать акцент на владение интерфейсом, на умение управлять
деятельностью: планировать, мониторить, корректировать, ставить цели,
комплексно, многосторонне оценивать их адекватность. Таким образом, трактовка математической
культуры как инфраструктуры для восприятия и обработки информации средствами
математики является конструктивной и позволяет переоценить имеющиеся факты, выявить
дидактически и методологически слабые места в учебно-методической литературе и
системе образования в целом.
В качестве примера рассмотрим ситуацию (с
которой мы сталкивались в процессе обучения), когда учащиеся в чертеже на
рис. 1 замечают равнобедренный треугольник ABC, но не только
не видят равнобедренный треугольник BAD, а даже после соответствующего
пояснения учителя высказывают сомнения в равнобедренности треугольника BAD.
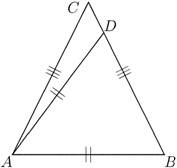
Рис. 1. Иллюстрация проблем с восприятием D ABD как
равнобедренного.
Причиной ошибки является тот факт, что
учащиеся сталкивались только со случаем, когда основание треугольника на
чертеже расположено горизонтально. Ошибка связана с недостаточной
сформированностью у учащихся геометрической культуры, поскольку они не осознали,
что в геометрии нет наблюдателя.
Подобная «негибкость», а на самом деле недостаток математической культуры, у
студентов экономических направлений может быть связана, например, с фиксацией
смысла обозначений и расположения значений величин на осях. Например, если
рассматривается зависимость капиталовложений K от некоторых параметров, одним из которых является
индекс потребительской уверенности (Consumer Confidence Index), обозначенный
как CCI, то выражение 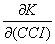 нередко не
воспринимается как частная производная функции K по переменной CCI,
поскольку в курсе математики студенты сталкивались только со случаем, когда
аргументы функции были однобуквенными. нередко не
воспринимается как частная производная функции K по переменной CCI,
поскольку в курсе математики студенты сталкивались только со случаем, когда
аргументы функции были однобуквенными.
Как проявление недостатка математической
культуры можно трактовать многочисленные примеры некорректностей в
использовании математического языка в общепринятых обозначениях.
Так, решив квадратное уравнение 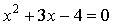 , часто пишут ответ: , часто пишут ответ: 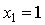 , , 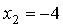 вместо более
корректного: вместо более
корректного: 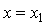 , , 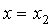 , где , где 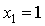 , , 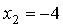 . .
Отождествление объекта с одним из
способов его задания – другой распространенный пример некорректности. Например,
отождествление функции с аналитическим выражением, обеспечивающим её
вычисление. Если в общепринятую формулу 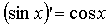 подставить
вместо x
число 1, получим подставить
вместо x
число 1, получим 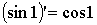 . Определение иррационального числа как бесконечной
непериодической дроби – ещё один подобный пример. . Определение иррационального числа как бесконечной
непериодической дроби – ещё один подобный пример.
Накопление некорректностей нередко
приводит к содержательным ошибкам и неспособности понять информацию. В связи с
этим заметим, что проявлением культуры преподавателя является внимание к
соглашениям «по умолчанию», к использованию математического слэнга. Обучение правильному
математическому слэнгу как проявлению математической культуры – тоже важная
дидактическая задача.
Оценить уровень математической культуры
несложно. Например, ответ на простой вопрос «что такое p?» говорит о
многом.
Отсутствие математической культуры,
опасность которого вызвана в том числе и информатизацией общества, может
привести и к такого рода «доказательствам»: 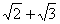 иррациональное число,
поскольку иррациональное число,
поскольку 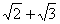 =1,41+1,73=3,14 – это число p, а это число
иррациональное! =1,41+1,73=3,14 – это число p, а это число
иррациональное!
Имманентной особенностью математической
культуры является отслеживание причинно-следственных связей, поскольку
процедура формального доказательства в математике рассматривается как условие
истинности математических утверждений. Примером проявления математической
культуры является реакция математика в случае обнаружения «контрпримера»:
настоящий математик ищет ошибку в доказательстве. Математическая культура
преподавателя математики проявляется и в его комментариях к своим действиям. Например,
при решении задачи «Найти значения параметра a, при которых уравнение 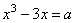 имеет три корня». имеет три корня».
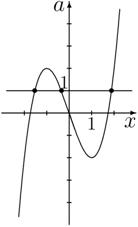
Рис. 2. Иллюстрация к задаче о нахождении
значений параметра a, при которых уравнение 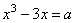 имеет три корня. имеет три корня.
Если после построения графика левой
части этого уравнения, см. рис. 2, учитель говорит «Нам нужны такие
значения параметра a, чтобы кривая 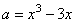 пересекалась с
горизонтальной прямой, отвечающей данному значению a, по трем
точкам», то, весьма вероятно, некоторые учащиеся не смогут раскрыть связь между
числом точек пересечения графиков и числом решений уравнения. Учитель с высоким
уровнем математической и педагогической культуры постарается выяснить, осознают
ли ученики эту связь. В данном варианте изложения это целесообразно сделать,
выбирая конкретные значения параметра a. Проблема с объяснением связана с опасным
отождествлением слова «переменная» со словосочетанием «значение переменной». В
самом деле, фразу a=1 большинство математиков однозначно воспринимает
как синоним фразы «значение параметра a равно 1», но на самом деле её можно
воспринять как утверждение о совпадении двух символов: буквы a и цифры 1
(цифра это тоже буква). Более того, нередко слово «цифра» в обыденной речи
воспринимается синонимично слову «число». Если в приведенном примере строить
графики линий пересекалась с
горизонтальной прямой, отвечающей данному значению a, по трем
точкам», то, весьма вероятно, некоторые учащиеся не смогут раскрыть связь между
числом точек пересечения графиков и числом решений уравнения. Учитель с высоким
уровнем математической и педагогической культуры постарается выяснить, осознают
ли ученики эту связь. В данном варианте изложения это целесообразно сделать,
выбирая конкретные значения параметра a. Проблема с объяснением связана с опасным
отождествлением слова «переменная» со словосочетанием «значение переменной». В
самом деле, фразу a=1 большинство математиков однозначно воспринимает
как синоним фразы «значение параметра a равно 1», но на самом деле её можно
воспринять как утверждение о совпадении двух символов: буквы a и цифры 1
(цифра это тоже буква). Более того, нередко слово «цифра» в обыденной речи
воспринимается синонимично слову «число». Если в приведенном примере строить
графики линий 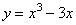 и y=a, то объяснение позволит
в сознании учеников зафиксировать фундаментальную связь между линией и её
уравнением. и y=a, то объяснение позволит
в сознании учеников зафиксировать фундаментальную связь между линией и её
уравнением.
В случае, когда данная связь фиксируется
формально, на уровне рефлекса, могут возникнуть проблемы с восприятием рассуждений.
Например, рассмотрим решение задачи «Найдите все такие значения параметра a, что
неравенство 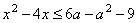 имело хотя бы одно
решение». Предложено графическое решение, основанное на представлении множеств
точек в системах координат xOy и aOy с совмещенными
осями Ox и Oy, заданных
неравенствами для координат этих точек: имело хотя бы одно
решение». Предложено графическое решение, основанное на представлении множеств
точек в системах координат xOy и aOy с совмещенными
осями Ox и Oy, заданных
неравенствами для координат этих точек: 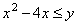 (область под
соответствующей параболой) и (область под
соответствующей параболой) и 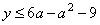 (область над
соответствующей параболой), см. рис. 3. В этом случае исходное неравенство
выполняется тогда и только тогда, когда для точки из второй области найдется
хотя бы одна точка в первой области, находящаяся выше неё (расположение этих
точек по горизонтали несущественно). Следовательно, требуемые значения a можно
интерпретировать как абсциссы тех точек на параболе (область над
соответствующей параболой), см. рис. 3. В этом случае исходное неравенство
выполняется тогда и только тогда, когда для точки из второй области найдется
хотя бы одна точка в первой области, находящаяся выше неё (расположение этих
точек по горизонтали несущественно). Следовательно, требуемые значения a можно
интерпретировать как абсциссы тех точек на параболе 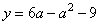 , которые находятся не ниже хотя бы одной точки на параболе , которые находятся не ниже хотя бы одной точки на параболе 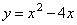 . .
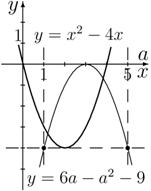
Рис. 3. Иллюстрация к задаче о нахождении таких
значений параметра a, что неравенство 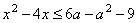 имело хотя бы одно
решение. имело хотя бы одно
решение.
Ошибка в восприятии этих рассуждений
обычно связана с некритичным отношением к расположению точек: в данном случае
переменные x
и a независимы,
поэтому взаимное расположение точек на параболах по горизонтали несущественно,
важно лишь их расположение по вертикали. Попытка совмещения осей вызывает
недоумение, сопровождающееся попытками использовать информацию о точках
пересечения парабол. Но последние не имеют отношения к рассматриваемой задаче.
Для оценки уровня математической
культуры важным является такой феномен как «понимание». Что значит «понять»? На
самом деле понимание включает в себя 3 компонента: 1) формирование
субъективной модели изучаемой информации, достаточно адекватной соответствующей
объективной модели; 2) установление интерфейсов с другими моделями,
сформированными в сознании субъекта; 3) включение модели или системы
моделей, представленных в данной информации, в систему субъективных моделей,
сформированных в сознании субъекта (например, в качестве элемента, компонента,
причины или следствия и др. Систему субъективных моделей и механизм работы
с ними мы будем называть инфраструктурой
работы с информацией. Повышение образованности и математической культуры
включает в себя, во-первых, формирование новой субъективной модели (или системы
моделей), во-вторых, включение этих моделей в систему уже имеющихся
субъективных моделей, в-третьих, развитие на этой основе механизма работы с
новыми моделями: механизмов восприятия, обогащения (вообще говоря,
субъективного), анализа, комплексной оценки (в том числе эстетической,
утилитарной и др.), применения.
В качестве примера формирования новой
субъективной модели можно привести развитие ситуации с теорией вероятностей:
специализированный язык, язык теории множеств. По-видимому, эта идея привела Л. Заде [23]
к теории нечетких множеств. Теория векторного, скалярного, тензорного поля,
которые зародились из математического анализа и геометрии. «Определение»
векторного поля как «области пространства…». Некорректности, возникающие и
фиксируемые в прикладной математике (понятие тензора). «Сначала я не понимал, а
потом привык» ‑ это значит, «встроил в систему субъективных моделей».
Культура включает в себя систему
шаблонов поведения, шаблонов и механизмов восприятия и обработки информации.
Под «обработкой информации» понимается, в том числе, и представление и передача
информации другому субъекту деятельности, причём на определенном уровне
сформированности данного вида культуры у этого субъекта деятельности в
состав этой информации может (и, возможно, должна) входить и система способов и
механизмов обработки информации.
Следовательно, в процессе обучения
математике следует формировать у обучаемого не только знания о конкретных
математических объектах, но и формировать способность (на том или ином уровне)
осуществлять обработку информации методами математики или хотя бы формировать
представление об этих способах обработки информации, не ограничиваясь
вычислениями. Примером использования математической культуры в художественной
литературе является речь Витьки Корнева в лаборатории в новогоднюю ночь из
повести «Понедельник начинается в субботу» братьев Стругацких.
«— Э, нет, — возразил я. — Так не пойдёт.
— А как? — жадно спросил Витька.
— Выметайся отсюда, — сказал я. — Покинь помещение.
— Куда?
— Куда хочешь.
Он перелез через диван и сгрёб меня за грудки.
— Ты меня слушай, понял? — сказал он угрожающе. — На
свете нет ничего одинакового. Всё распределяется по гауссиане. Вода воде рознь…
Этот старый дурак не сообразил, что существует дисперсия свойств…».
Математическая культура выпускника важна
и как компонент мышления. Математические структуры (Бурбаки) и структуры
мышления тесно взаимосвязаны. Важна и коммуникативная роль математической
культуры. Математическая культура – это источник интеллектуального опыта, что
обусловлено древностью математики как науки, сочетающей в себе сугубо
прикладной и абстрактно-теоретический аспекты.
Выделим ещё несколько функций
математической культуры, которые следует учитывать при организации процесса
обучения математике:
‑ математическая культура как
система применения математики для решения прикладных и теоретических задач [24];
‑ математическая культура как
система целеполагания и оценочной деятельности (например, «красивая теорема»,
«изящное решение» и др.);
‑ математическая культура как
средство воспитания.
Заключение
Проведенное нами исследование позволяет
сделать следующие основные выводы.
1. Математическая культура
выпускника и специалиста остается одним из ключевых компонентов культуры
современного общества.
2. Профессиональная компетентность выпускника
и специалиста включает в себя культурный компонент, неотъемлемой частью
которого является математическая культура.
3. Специальным образом
организованное математическое образование в экономическом университете,
опирающееся на модель математической культуры как инфраструктуры восприятия и
обработки информации и обмена информацией, состоит из системы феноменов,
системы отношений, системы интерфейсов и системы управления, позволяет успешно
решать задачу повышения профессиональной компетентности выпускника.
References
1. Komissarova, E. S. Matematicheskaya kul'tura i ee rol' v formirovanii, interpretatsii i realizatsii pravovykh norm / E. S. Komissarova // Yuridicheskaya tekhnika.—2016.—№ 10.—S. 585–587.
2. Bulatova, E. G. Matematicheskaya kul'tura kak sistemnaya kategoriya / E. G. Bulatova, Iskanderova A. B., Snigireva T. A. // Aktual'nye problemy gumanitarnykh i estestvennykh nauk. — 2015. — № 12-4. — S. 76–81.
3. Evdokimova, G. S. Matematicheskaya kul'tura — vysshee proyavlenie obrazovannosti i professional'noi kompetentnosti / G. S. Evdokimova, V. D. Bochkareva // Vestnik Mordovskogo universiteta. — 2015.— T. 25, № 1.— S. 37–43.
4. Unaisarova, R. D. Pedagogicheskie osnovy ponyatiya «matematicheskaya kul'tura studentov». / R. D. Unaisarova, S. N. Sushkova // Vestnik Orenburgskogo gosudarstvennogo pedagogicheskogo universiteta. Elektronnyi nauchnyi zhurnal.— 2008.— № 1.— S. 134–139.
5. Voronina, L. V. Matematicheskaya kul'tura lichnosti / L. V. Voronina, L. V. Moiseeva // Pedagogicheskoe obrazovanie v Rossii.—2012.— № 3.—S. 37–45.
6. Urtenova, A. U. Matematicheskaya kul'tura: struktura i soderzhanie / A. U. Urtenova, N. S. Urtenov // Sibirskii pedagogicheskii zhurnal.—2014.—№ 2.—S. 51–56.
7. Shcherbakov, R. N. Matematicheskaya kul'tura uchashchegosya / R. N. Shcherbakov // Pedagogika.—2013.—№ 4.—S. 57–65.
8. Pantseva, E. Yu. Matematicheskaya kul'tura — osnova tvorcheskogo potentsiala spetsialista / E. Yu. Pantseva // Nauka — promyshlennosti i servisu.—2012.—№ 2.—S. 315–321.
9. Rozanova, S. A. Matematicheskaya kul'tura studentov vysshikh uchebnykh zavedenii estestvennonauchnogo i inzhenerno-tekhnicheskogo profilei / S. A. Rozanova // Vestnik rossiiskogo universiteta druzhby narodov. Seriya: Fundamental'noe estestvennonauchnoe obrazovanie.—2003.—№ 8.—S. 41–51.
10. Lipatnikova, I. G. Sovremennye podkhody k soderzhaniyu matematicheskogo obrazovaniya v kontekste dialoga kul'tur / I. G. Lipatnikova // Pedagogicheskoe obrazovanie v Rossii. — 2015. — № 7. — S. 152–159.
11. Dubynina, T. V. Matematicheskaya kul'tura kak element sovremennogo obrazovaniya / T. V. Dubynina // Vestnik Yuzhno-Ural'skogo gosudarstvennogo universiteta. Seriya: Obrazovanie. Pedagogicheskie nauki.—2010.—№ 3 (179).—S. 114–120.
12. Zainiev, R. M. Matematicheskaya kul'tura — osnova podgotovki inzhenera / R. M. Zainiev // Vysshee obrazovanie segodnya.—2009.— № 5.— S. 48–50.
13. Evdokimov, P. A. O matematicheskoi kul'ture v vysshem professional'nom obrazovanii / P. A. Evdokimov // Materialy nauchno-metodicheskoi konferentsii severo-zapadnogo instituta upravleniya. — Rossiiskaya akademiya narodnogo khozyaistva i gosudarstvennoi sluzhby pri Prezidente Rossiiskoi Federatsii (Moskva), 2012. — № 1.—S. 120–131.
14. Pantseva, E. Yu. Matematicheskaya kul'tura — aspekt professional'noi kul'tury / E. Yu. Pantseva // Nauchno-metodicheskii elektronnyi zhurnal Kontsept.—2014.—T. 20.—S. 1496–1500.
15. Banks, J. A. Multicultural education / J. A. Banks, C. A. McGee Banks.— Needham Heights, MA: Allyn & Bacon, 1989.
16. Bishop, A. Mathematical enculturation: a cultural perspective on mathematics education / A. Bishop.—Dordrecht: Kluwer, 1991.
17. Hofstede, G. National cultures and corporate cultures / G. Hofstede // In L. A. Samovar & R. E. Porter (Eds.), Communication between cultures.— Belmont, CA: Wadsworth, 1984.
18. Tarasova, M. V. Kul'tura i obrazovanie: printsipy vzaimodeistviya : monografiya / M. V. Tarasova .— Krasnoyarsk : Sib. feder. un-t, 2012, 360 s.
19. Uspenskii, V.A. Matematicheskoe i gumanitarnoe: preodolenie bar'era / Predislovie k matematike [sb. statei]. SPb. : Amfora, 2015. S. 5 51.
20. Vyzhletsov, G. P. Aksiologiya kul'tury/ G.P.Vyzhletsov// SPb.: SPbGU. – 1996. S.66
21. Pelipenko, A.A. Kul'tura kak sistema / A.A. Pelipenko, I.G. Yakovenko // M.: Yazyki russkoi kul'tury, 1998, 396 s.
22. Mel'nikov, Yu.B. Matematicheskoe modelirovanie: struktura, algebra modelei, obuchenie postroeniyu matematicheskikh modelei: Monografiya / Yu.B. Mel'nikov. Ekaterinburg: Ural'skoe izdatel'stvo, 2004, 384 s.
23. Zadeh, L. Fussy sets / L. Zadeh // Inf. Control.— 1965.— Vol. 8.— P. 338–353.
24. Odinets, V. P. Ob istorii pervoi ekspertnoi sistemy po atributsii i datirovke predmetov zhivopisi / V. P. Odinets // Trudy XIII mezhdunarodnykh Kolmogorovskikh chtenii : sbornik statei. — Yaroslavl' : RIO YaGPU, 2015.—S. 29–36.
Link to this article
You can simply select and copy link from below text field.
|





