|
MAIN PAGE
> Back to contents
Cybernetics and programming
Reference:
Komarova A.V., Korobeynikov A.G., Menshchikov A.A., Klyaus T.K., Negol's A.V., Sergeeva A.A.
Theoretical possibilities for combining various mathematical primitives within an electronic digital signature scheme.
// Cybernetics and programming.
2017. № 3.
P. 80-92.
DOI: 10.25136/2644-5522.2017.3.23364 URL: https://en.nbpublish.com/library_read_article.php?id=23364
Theoretical possibilities for combining various mathematical primitives within an electronic digital signature scheme.
Komarova Antonina Vladislavovna
Graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
196244, Russia, Saint Petersburg, ul. Tipanova, d. 29

|
piter-ton@mail.ru
|
|
 |
Korobeynikov Anatolii Grigor'evich
Doctor of Technical Science
Professor, Department of Design and Security of Computer Systems, St. Petersburg National Research University of Information Technologies, Mechanics
196631, Russia, g. Saint Petersburg, ul. Kronverkskii Prospekt, 49

|
korobeynikov_a_g@mail.ru
|
|
 |
Menshchikov Aleksandr Alekseevich
Graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, Saint Petersburg, Kronverkskii prospekt, 49

|
menshikov@corp.ifmo.ru
|
|
 |
Klyaus Tat'yana Konstantinovna
Graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, g. Saint Petersburg, Kronverskkii prospekt, 49

|
t_klyaus@corp.ifmo.ru
|
|
 |
Negol's Aleksandr Valer'evich
Graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, g. Saint Petersburg, ul. Kronverkskii Prospekt, 49

|
dozory07@yandex.ru
|
|
 |
|
Sergeeva Anastasiya Aleksandrovna
Graduate student, St. Petersburg National Research University of Information Technologies, Mechanics and Optics
197101, Russia, Saint Petersburg, Kronverkskii prospekt, 49

|
aasergeeva@corp.ifmo.ru
|
|
 |
|
DOI: 10.25136/2644-5522.2017.3.23364
Received:
19-06-2017
Published:
26-07-2017
Abstract:
The study is devoted to the algorithms and protocols of an electronic digital signature, providing for the key information properties: its integrity, authenticity and accessibility. This article highlights the problems of modern cryptography and a possible way to solve them via creation of an electronic digital signature that can withstand a quantum computer. The article concerns various mathematical primitives, which can increase the stability of existing cryptosystems when used together. This area of research is a new and promising one for the development of domestic cryptography. The theoretical methods of research used in this article include the theory of computational complexity, the theory of rings, fields and lattices, algorithmic aspects of lattice theory and their application in cryptography, in particular, the complexity of solving systems of linear Diophantine equations, the complexity of finding the shortest nonzero lattice vector And the vector of the lattice closest to the given vector, known approximate algorithms for these problems. We refer to experimental methods of research, such as carrying out statistical calculations and data analysis in the Mathlab mathematical environment, constructing elliptic curves in the mathematical environment of Mathcad, creating software implementations of the algorithm for generating a signature in Python, using precompiled modules from the NumPy library. It is planned to achieve the following results in the future: 1. The development of a methodology for constructing electronic digital signature schemes based on two independent computationally difficult problems; 2. The development of a polynomially complex electronic digital signature scheme based on fundamentally different mathematical primitives; 3. The estimation of the size of safe parameters of the developed EDS protocols; 4. The theoretical model of the growth of calculation time from the length of an electronic digital signature key.
Keywords:
information privacy, Pollard algorithm, discrete logarithming, the shortest vector problem, postquantum cryptography, cryptosystem, the lattice theory, elliptic curve, information security, digital signature
This article written in Russian. You can find original text of the article here
.
Введение Введение
Информационные технологии с каждым годом все больше набирают свою значимость в современном мире. Для успешного функционирования любых организаций, будь то коммерческие или государственные структуры, требуется непрерывная защита циркулирующей в них информации. Существуют проблемы обеспечения аутентификации информации, обеспечения аутентичности информации и обеспечения конфиденциальности информации. Как известно, все эти задачи решаются с помощью электронной цифровой подписи (далее - ЭЦП). В связи с этим, постоянная доработка и модернизация существующих алгоритмов и стандартов ЭЦП имеет определяющее значение для функционирования государственных и коммерческих организаций. Стойкость всех криптографических алгоритмов ЭЦП основывается на трудности решения определенной криптографической задачи. Так, известный во всем мире криптографический алгоритм RSA основан на задаче факторизации. А схема Эль-Гамаля, как известно, основана на задаче дискретного логарифмирования в простом конечном поле. Трудоемкими для взлома в настоящий момент считаются алгоритмы и протоколы, основанные на задаче дискретного логарифмирования на эллиптических кривых (далее – ЭК) [1].
Также хочется отметить возрастающий интерес к алгоритмам, предположительно стойким к квантовым вычислениям, так называемым алгоритмам «постквантовой криптографии» [2]. В частности, к таким протоколам можно отнести протоколы цифровой подписи: Гольдвассера-Гольдштейна-Халеви (GGH) [3], Миссиансио-Вадхена [4], Миссиансио-Любашевского [5], NTRUSign [6] и др. Таким образом, для повышения трудоемкости взлома, предлагается использовать алгоритм, основанный одновременно на двух вычислительно сложных задачах, а именно на примитивах теории решеток, относящейся к постквантовой криптографии, и на задаче дискретного логарифмирования на эллиптических кривых (ЭК). Проблемы современной криптографии В настоящее время в современной криптографии существуют следующие проблемы:
- Ограниченное количество основополагающих «трудных» задач, на которых базируются используемые схемы. Данное ограничение ведет к тому, что количество рабочих схем криптографии с открытым ключом весьма невелико.
- Увеличение необходимого размера для блока данных, а также ключей, связанные с прогрессом математики, а также вычислительной техники.
- Потенциальная ненадежность базиса. На данный момент рассматривается возможность решение задачи данного типа за полиномиальное время. Теория вычислительной сложности уже доказала связь вычислительно сложных задач между собой. Данное доказательство означает, что если хотя бы на одну из современных криптосистем будет проведена успешная атака, то и большинство остальных систем могут не устоять.
- Проблема криптографии в эру квантовых компьютеров. Алгоритм Шора утверждает, что после наступления эры квантовых компьютеров, многие криптографические схемы могут потерять свою актуальность в связи со значительным увеличением вычислительной мощи [1].
Из всего вышесказанного необходимо сделать вывод, что в настоящее время наиболее актуальная проблема в сфере современной криптографии – это повышение стойкости и уменьшения размера блоков данных путем модификации уже существующих криптосистем. Процедура формирования электронной цифровой подписи Схема ЭЦП общепринято состоит из трех основных этапов [7]:
- Генерация ключей (подписи и проверки);
- Формирование подписи;
- Проверка подписи.
Далее представим описание процедур формирования и проверки ЭЦП в общем виде.
Для того чтобы подписать некоторое сообщение M, пользователь должен сгенерировать секретный ключ х и по нему сформировать открытый ключ y, который будет храниться в справочнике открытых ключей в открытом доступе. Эта процедура выполняется один раз при вычислении или смене секретного ключа. Специальный алгоритм Sign, на вход которого подаются подписываемое сообщение М и секретный ключ х, формирует подпись S к сообщению М. Данный процесс проиллюстрирован на рисунке 1.
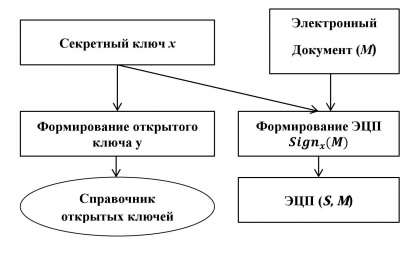
Рисунок 1. Общая схема процедуры формирования ЭЦП S к сообщению M
Для выполнения процедуры проверки подписи к сообщению М пользователь получает открытый ключ у автора сообщения, находя его в справочнике открытых ключей. Далее он с помощью специального алгоритма проверки подписи Verify, на вход которого подаются сообщение М, подпись S к нему и открытый ключ у подписывающего производит проверку, является ли автор сообщения тем, за кого себя выдает. Если алгоритм Verify возвращает положительный ответ, то владелец открытого ключа у признается автором ЭЦП к сообщению М.
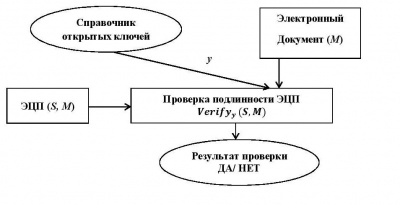
Рисунок 2. Общая схема процедуры проверки подлинности ЭЦП S к сообщению M
Схематично подписанное сообщение, согласно ГОСТ Р 34.10-2012 «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи» можно представить так, как показано на рисунке 3 [7].
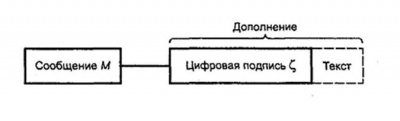
Рисунок 3. Схематическое представление подписанного сообщения
ЭЦП относится к условно стойким криптографическим преобразованиям, т.к. их стойкость основывается на высокой вычислительной сложности решения некоторой криптографической задачи.
Под вычислительно сложной или трудной задачей понимается задача, которая имеет решение, однако его нахождение требует больших вычислительных ресурсов и временных затрат. Среднее количество операций, которые необходимо совершить, чтобы найти решение с помощью лучшего алгоритма, принимается за количественную меру сложности трудно решаемой задачи. Проблема оценки сложности задачи заключается в ее зависимости от поиска наилучшего алгоритма решения. Теория решеток и ее преимущества Теория решеток частично применялась при создании и разработке компьютеров, однако, активное распространение, теория получила лишь в последнее время. Основная область применения теории решеток – создание алгоритмов, устойчивых к атакам с помощью квантовых компьютеров. Изучает теорию решеток особая область криптографии – постквантовая криптография. Алгоритмы с использованием теории решеток, рассматриваемые в данном проекте, являются наиболее перспективными ее направлениями.
Криптографические примитивы на основе задач теории решеток обладают очень сильной криптостойкостью, основанной на доказательстве «в наихудшем случае». Появление квантовых компьютеров, которые способны обрушить всю современную асимметричную криптографию, никак не повлияет на криптостойкость подобных примитивов. Также, они сравнительно эффективно выполняются на компьютерах. И наконец, такие примитивы чрезвычайно просты в своей формулировке.
Криптостойкость алгоритмов с использованием решеток, как и современных алгоритмов асимметричной криптографии, основана на трудной математической задаче [2].
Решетка – это совокупность точек в n-мерном пространстве с периодической структурой [5]. Более точно решетку L можно определить как абелеву подгруппу, заданную в пространстве Rm.
Пусть базис решетки `B={b_(1)... b_(n)}` задан линейно независимыми векторами, тогда под решеткой будем понимать множество целочисленных линейных комбинаций этих векторов.
К трудным задачам теории решеток можно отнести следующие:
1. Задача поиска наикратчайшего вектора решетки - SVP (Shortest vector problem). По базису решетки B требуется найти кратчайший ненулевой вектор x, принадлежащий этой решетке (Рис.4). SVP-задача является NP-полной задачей, и является наиболее перспективной для использования в протоколах безопасности [8].
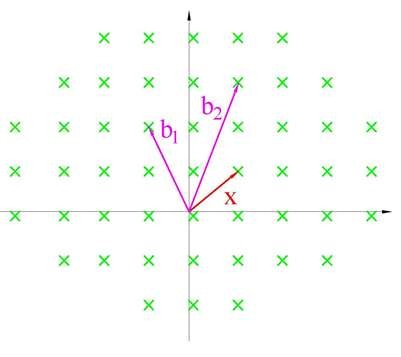
Рисунок 4. Поиск кратчайшего вектора решетки
2. Задача приближенного поиска кратчайшего вектора решетки - `SVP_(Gamma)` (γ -approximation shortest vector problem). По базису решетки B и вещественному γ>0 требуется найти ненулевой вектор x, принадлежащий этой решетке, с p-нормой (Рис.5).
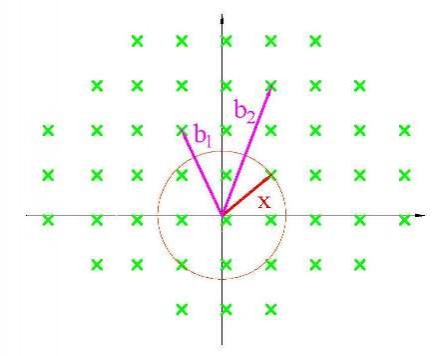
Рисунок 5. Приближенный поиск кратчайшего вектора решетки
3. Задача поиска ближайшего вектора решетки - CVP (Closest vector problem). По базису решетки B и некоторому векторуy требуется найти ближайший к y вектор x, принадлежащий этой решетке (Рис.6).
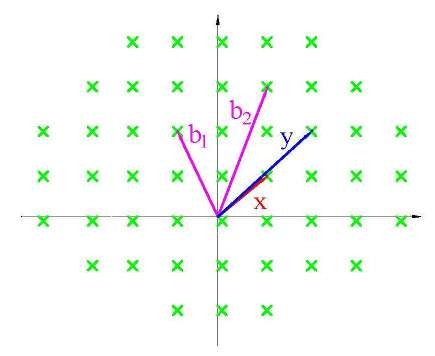
Рисунок 6. Поиск ближайшего вектора решетки
4. Задача приближенного поиска ближайшего вектора решетки - `CVP_(Gamma)` (γ - approximate closes vector problem). По базису решетки B, вещественному γ>0 и некоторому векторуy требуется найти ближайший к y вектор x, принадлежащий этой решетке, с p-нормой (Рис.7).
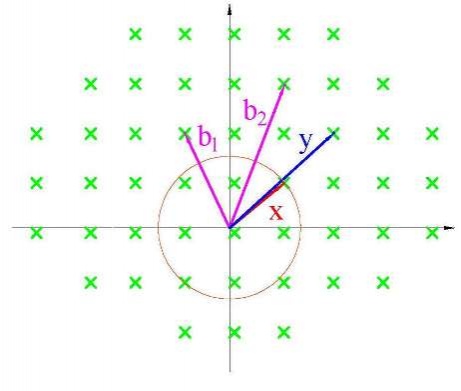
Рисунок 7. Приближенный поиск ближайшего вектора решетки
5. Задача поиска уникального кратчайшего вектора – `uSVP_(gamma)` (γ - approximate unique shortest vector problem). По базису решетки, в которой кратчайший вектор x в k раз меньше другого кратчайшего линейно независимого вектора y, необходимо найти кратчайший вектор (Рис.8).
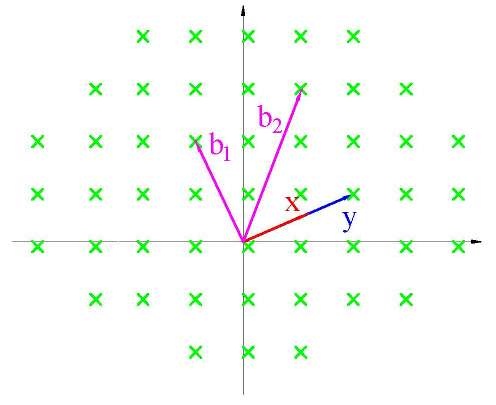
Рисунок 8. Поиск уникального кратчайшего вектора
6. Задача приближенного поиска кратчайших линейно независимых векторов - `SIVP_(gamma)` (γ - approximate shortest independent vector problem). Для данной n-мерной решетки требуется найти набор линейно-независимых векторов , принадлежащих решетке, с p-нормой (Рис.9).
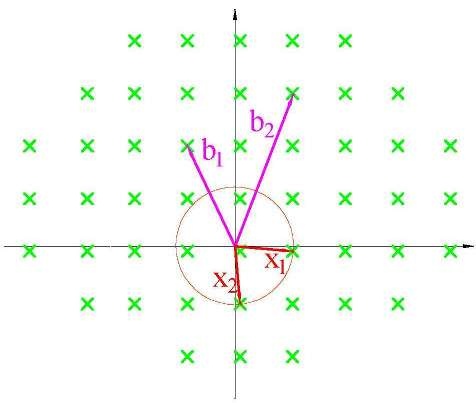
Рисунок 9. Приближенный поиск кратчайших линейно независимых векторов Актуальность построения схем на эллиптических кривых В 1985 году Нил Коблиц и Виктор Миллер независимо предложили использовать в криптографии некоторые алгебраические свойства эллиптических кривых (ЭК). С этого момента началось бурное развитие нового направления в криптографии, для которого используется термин криптография на ЭК. В настоящее время лучшие алгоритмы имеют экспоненциальное время работы, в отличие от алгоритмов для решения проблемы простого дискретного логарифма и проблемы факторизации целого числа, которые имеют субэкспоненциальное время работы. Это означает, что в системах на ЭК желаемый уровень безопасности может быть достигнут при значительно меньшей длине ключа, а для современной криптографии актуальна проблема повышения стойкости и уменьшения размера блоков данных [9].
В общем случае для нахождения дискретного логарифма на ЭК можно использовать все универсальные методы дискретного логарифмирования, которые не используют специфических свойств структуры группы. Специфических алгоритмов на ЭК пока не придумано, благодаря этому ЭЦП на ЭК является наиболее стойкими при заданном уровне сложности генерации подписи. Наиболее эффективными считаются алгоритмы Сильвера-Полига-Хеллмана [10] и p-метод Полларда [11]. Сложность первого алгоритма по времени `W(t)=O(logp)^(c)`, а по памяти `W(m)=Osqrt(r)` . p-метод Полларда имеет аналогичную сложность по памяти, но меньшую сложность по времени: `W(m)=Olog(p)`. В обоих случаях r – это наибольший простой делитель порядка мультипликативной группы p-1, с – положительная константа.
Следует отметить, что стойкость действующих государственных стандартов Российской Федерации ГОСТ Р 34.10-2012 «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи» [7], а так же ГОСТ Р 34.11-2012 «Информационная технология. Криптографическая защита информации. Функция хэширования» [12] основана именно на задаче дискретного логарифмирования на эллиптических кривых. Обсуждение предложенного подхода В основе безопасности современных схем ЭЦП лежит решение некоторой вычислительно сложной задачи. Такая задача относится к классу NP недетерминированных полиномиальных задач. В случае, если в процессе решения данного класса задач не используется дополнительная информация, временная сложность их решения является полиномиально неограниченной. В теории вычислительной сложности существует гипотеза о том, что задачи класса NP не могут быть решены за полиномиальное время. В данный момент эта гипотеза не разрешена. Это позволяет прийти к выводу о том, что отсутствие существования эффективного способа решения некоторой вычислительно сложной задачи пока не доказано.
Анализ представленных выше математических примитивов позволяет сказать, что безопасность алгоритмов ЭЦП зависит от двух факторов:
1. От текущей стойкости алгоритма, зависящей от сложности лучшего из известных методов решения трудной задачи, положенной в основу алгоритма;
2. От вероятности непредвиденного взлома, т.е. вероятности появления принципиально новых, имеющих сравнительно низкую трудоемкость методов и алгоритмов решения базовой вычислительно трудной задачи.
Вероятность нахождения атаки, сложность проведения которой значительно ниже сложности решения базовой вычислительно трудной задачи, может быть найдена с помощью метода экспертных оценок. Несмотря на то, что значение данной вероятности представляет сбой некоторое малое значение, для обеспечения необходимого уровня безопасности ЭЦП целесообразно применять схемы, в основе которых заложено одновременно две вычислительно трудные задачи. При следующих значениях вероятностей появления алгоритмов, позволяющих эффективно находить решения базовых вычислительно трудных задач:
Р (взлом задачи поиска наикратчайшего вектора решетки) `cong10^(-8)` ;
Р (взлом задачи дискретного логарифмирования на ЭК) `~=10^(-8)` .
Вероятность одновременного взлома задачи поиска наикратчайшего вектора решетки и задачи дискретного логарифмирования на ЭК равна произведению вероятностей взлома каждой задачи в отдельности, а именно `cong10^(-16)`.
Это означает, что в схемах ЭЦП, основанных на двух трудных задачах, может быть существенно повышен уровень их безопасности. Использование алгоритмов ЭЦП, взлом которых требует одновременного решения двух вычислительно трудных задач, является предпочтительным в ряде сфер человеческой деятельности, требующих обеспечения высокого уровня информационной безопасности (военной, банковской и т.д.).
Механизм комбинирования двух вычислительно трудных задач в одной схеме был предложен в работе [13], поэтому предложенный авторами подход представляется интересным и возможным в реализации.
В работах [14-16] представлены некоторые алгоритмы и протоколы ЭЦП, одновременно опирающиеся на сложность нескольких трудных задач. Это как протоколы коллективной подписи [14], так и новые алгоритмы [15, 16]. Следует отметить, что в данных работах освещаются вопросы комбинирования в одной схеме двух трудных задач, относящихся к асимметричной криптографии.
Авторы данной статьи предлагают использовать задачу постквантовой криптографии для повышения стойкости схем ЭЦП. Данный подход актуален не только в силу возможного появления квантового компьютера, но и для повышения стойкости современных алгоритмов к криптоанализу и к растущим вычислительным мощностям. Заключение В данной работе рассматривается подход к комбинированию двух различных математических примитивов в одной схеме электронной цифровой подписи. Это задача поиска наикратчайшего вектора решетки (Shortest Vector Problem) и задача дискретного логарифмирования на эллиптических кривых. Также в статье освещается актуальность данного вопроса для современной криптографии. В силу важности проблемы, авторы полагают, что данная статья может быть интересна для обсуждения даже на теоретическом уровне. В будущем авторами планируется реализация данного подхода и создание рабочего алгоритма электронной цифровой подписи.
References
1. Piskova A.V., Korobeinikov A.G. Razrabotka algoritma elektronnoi tsifrovoi podpisi, osnovannogo na zadachakh faktorizatsii i diskretnogo logarifmirovaniya na ellipticheskikh krivykh // Sbornik trudov IV Vserossiiskogo kongressa molodykh uchenykh SPb.: Universitet ITMO, 2015. S. 322–326.
2. Piskova A.V. Usilenie stoikosti skhemy autentifikatsii informatsii putem resheniya neskol'kikh vychislitel'no slozhnykh zadach // Nauchnye raboty uchastnikov konkursa "Molodye uchenye NIU ITMO" 2015 goda. 2016. S. 234-237.
3. Goldreich O, Goldwasser, Halevi S. Public-key cryptosystems from lattice reduction problems.-In Advances in cryptology. Lecture Notes in Computer Science. – №1294. – 1997. – p. 112-131.
4. Micciancio D., Vadhan S. Statistical zero-knowledge proofs with efficient provers: lattice problems and more. In Advances in cryptology. Lecture Notes in Computer Science. – 2003. – p. 282-298.
5. Lyubashevsky V., Micciancio. Asymptotically efficient lattice-based digital signatures. Lecture in Computer Science. – 2008. – №4948. – p. 379–396.
6. Hoffstein J., Graham N. A. H., Pipher J., Silverman J. H., Whyte W. NTRUSIGN: Digital signatures using the NTRU lattice. – In Proc. of CT-RSA, LNCS. – №2612. – 2003. – p. 122–140.
7. GOST R 34.10-2012. Natsional'nyi standart Rossiiskoi Federatsii. «Informatsionnaya tekhnologiya. Kriptograficheskaya zashchita informatsii. Protsessy formirovaniya i proverki elektronnoi tsifrovoi podpisi», 2012.
8. Piskova A.V., Korobeinikov A.G. Osobennosti primeneniya teorii reshetok v skhemakh elektronnoi tsifrovoi podpisi // Kibernetika i programmirovanie. 2016. № 2. S. 8-12.
9. Piskova A.V. Teoriya reshetok i ee primenenie v postkvantovoi kriptografii // Sbornik tezisov dokladov V Vserossiiskogo kongressa molodykh uchenykh. 2016. S. 87.
10. S. C. Pohlig and M. E. Hellman An Improved Algorithm for Computing Logarithms Over GF(p) and its Cryptographic Significance // IEEE Transactions on Information Theory. — 1978. — Vol. 1, no. 24. — P. 106-110.
11. O. N. Vasilenko. Teoretiko-chislovye algoritmy v kriptografii. — M.: MTsNMO, 2003. — 328 s. — 1000 ekz. — ISBN 5-94057-103-4.
12. GOST R 34.11-2012. Natsional'nyi standart Rossiiskoi Federatsii. «Informatsionnaya tekhnologiya. Kriptograficheskaya zashchita informatsii. Funktsiya kheshirovaniya», 2012.
13. Moldovyan, D.N. Dvukhklyuchevye kriptosistemy s novym mekhanizmom formirovaniya tsifrovoi podpisi [Tekst] / D.N. Moldovyan, N.A. Moldovyan // Upravlenie zashchitoi informatsii. 2006. T. 10. № 3. S. 307–312.
14. Dernova E.S., Moldovyan N.A. Protokoly kollektivnoi tsifrovoi podpisi, osnovannye na slozhnosti resheniya dvukh trudnykh zadach // Bezopasnost' informatsionnykh tekhnologii. 2008 №2. S 79-85.
15. Dernova, E.S. Sintez algoritmov tsifrovoi podpisi na osnove neskol'kikh vychislitel'no trudnykh zadach [Tekst] / E.S. Dernova, N.A. Moldovyan // Voprosy zashchity informatsii. 2008. № 1. S. 22–26.
16. Dernova E.S., Moldovyan N.A. Novyi algoritm ETsP, raskrytiya kotorogo trebuet odnovremennogo resheniya dvukh trudnykh zadach // Innovatsionnaya deyatel'nost' v Vooruzhennykh silakh Rossiiskoi Federatsii: Trudy vsearmeiskoi nauchno-prakticheskoi konferentsii. 22-23 noyabrya 2007 g, SanktPeterburg. SPb.: VAS, 2007. C. 229-233
Link to this article
You can simply select and copy link from below text field.
|
|





