|
MAIN PAGE
> Back to contents
Philosophical Thought
Reference:
Lipov A.N.
About the “incommensurate entities” in the philosophy of Pythagoreans. To the philosophical grounds of irrational proportions in science and culture
// Philosophical Thought.
2018. № 11.
P. 93-110.
DOI: 10.25136/2409-8728.2018.11.26855 URL: https://en.nbpublish.com/library_read_article.php?id=26855
About the “incommensurate entities” in the philosophy of Pythagoreans. To the philosophical grounds of irrational proportions in science and culture
Lipov Anatolii Nikolaevich
PhD in Philosophy
research assistant at Institute of Philosophy of the Russian Academy of Sciences
119 330, Russia, g. Moscow, ul. Mosfil'movskaya, 41, of. 54

|
antolip@yandex.ru
|
|
 |
Other publications by this author
|
|
|
DOI: 10.25136/2409-8728.2018.11.26855
Received:
13-07-2018
Published:
20-11-2018
Abstract:
The subject of this research is the philosophical grounds that predetermined the discovery of proof of the existence of incommensurate or irrational magnitudes in the philosophy of Pythagoreans at the time when the very notion of irrationality was an anathema for those suggesting that the numbers were the rational entities underlying the Universe. Therefore, it became possible to express both, physical and cultural-aesthetic consistencies, by the similar to each other mathematical rows and geometrical proportions that predetermines the calculation methods for harmonic structures, uninterrupted proportions and limiting values – the first premise to the structure of ancient teaching on formation. Based on the interdisciplinary analysis and comparative method of research, the article analyzes the history of discovery of the phenomenon of incommensurability and irrationality. A conclusion is made that back in Pythagoras’ times, this discovery led to the need for substantial transformation of the entire fabric of elementary geometry in anticipation of structuring the general theory of proportions, causing the first in history crisis of ancient philosophy and mathematics. The author also substantiates and traces the discovered by Pythagoreans correlation between the irrational proportions and irrational mathematical constant of “golden ratio” that underlies the architectural proportions in the history of culture, as well as reflected in various regularities and spheres of human existence – science, culture, architecture, and art. Among the main conclusion is also the author’s hypothesis that universality of the irrationality of magnitudes of “golden ration” and their prevalence in the diverse natural and cultural regularities up to the present encourages the pursuance of meanings, which would unite them into a certain common theory that generalizes and expresses the structure of global constants.
Keywords:
Pythagorean philosophy, proportional harmonic relations, incommensurable entities, irrational numbers, irrational numerical relationships, irrational proportions, pentagram, pentagonal symmetry, golden section, ideal form principle
This article written in Russian. You can find original text of the article here
.
Одним из значительных открытий в пифагорейской школе на рубеже У-У11в.в. до н. э. стало и открытие явления несоизмеримости, т.е. обнаружение таких величин, отношение между которыми не могли быть выражено с помощью отношения целых чисел и которое по степени математической значимости можно сравнить, пожалуй, лишь с открытием дифференциального и интегрального исчислений И. Ньютоном и Г. Лейбницем. Именно последователи Пифагора заложили эмпирические основы музыкальной акустики и впервые сформулировали основные понятия и принципы музыкальной теории, в которых для древних греков условием некоего устойчивого совершенства и гармонии являлась необходимость обязательного присутствия пропорциональной связи или согласного строя.
По нашему убеждению, и мы попытаемся обосновать этот тезис далее, многие методологические трудности, с которыми столкнулось естествознание на рубеже двух тысячелетий, в той или иной степени связаны с загадками пифагорейцев и элеатов, заложивших основу гармонического и математического видения мира. Невзирая на то, что положение Пифагора о том, что числа правят миром, это положение воспринимается ныне не более как некая научная мета-метафора и сегодня, как и в древности, с особой значимостью встает вопрос о существовании особых (универсальных) математических отношений, воплощенных в организации реально наблюдаемых наукой объектов и явлений.
Ещё из школьной программы нам известно, что эта теорема Пифагора формулируется так – квадрат гипотенузы равен сумме квадратов катетов (с 2=а 2 + b2). Достаточно длительный период времени научный мир считал Пифагора родоначальником чистой математики, ибо именно он сделал первый шаг к сплошной математизации приобретенных знаний. Влияние Пифагора на мыслителей последующих эпох вплоть до Коперника и Кеплера и частота, с которой встречается его имя во всей античной литературе, может соперничать даже с Сократом и Платоном, далеко превосходя в этом отношении их предшественников.
Из античных источников следует, что последователи Пифагора знали три вида пропорций – арифметическую, геометрическую и гармоническую. Однако помимо данных пропорций пифагорейцы особое внимание уделяли и так называемым непрерывным пропорциям или предельными величинам, то есть таким пропорциям, у которых средние члены совпадали (в = с). При этом пифагорейцы не только изучали математические свойства так называемых «средних величин», но и наполняя их глубоким эстетическим смыслом.
Известно, что Демокриту (род. ок. 470 г. н.э.) принадлежит книга «Об иррациональных линиях и телах». Следовательно, к этому времени иррациональность √ 2 была уже доказана. Гипократ Хиосский (ок. 440 г. до н.э.) занимался в то время проблемой удвоения куба, решение которой должна было предшествовать и разрешению соответствующей проблемы в планиметрии – проблемы удвоения квадрата, тесно связанной с открытием несоизмеримых отрезков. Из чего можно заключить, что несоизмеримые или иррациональные отношения в это время занимали уже значительное место в греческой математической теории.
Из истории также известно, что сами греки полупрезрительно именовали египтян «натягивателями веревок», хотя уже во времена царя Хамураппи (ХУ111 в. до н.э.) вавилоняне умели решать не только линейные, квадратные, но и некоторые виды кубических уравнений, а также системы линейных и квадратных уравнений с двумя неизвестными. Невзирая на то, что все эти системы уравнений и формулы были растворены в контексте конкретных задач с конкретными же числовыми кооффициентами, не может быть никаких сомнений в том, что жрецы, математики и архитекторы Вавилона владели в том числе и их общими принципами и методами их решения. В Древнем Египте в эту эпоху умели решать только самые простые линейные уравнения.
Что касается геометрии Древнего Вавилона, то она не достигла таких крупных успехов как вавилонская алгебра, уже хотя бы на том основании, что известно, что вавилонское число π = 3 было существенно хуже египетского. Вавилоняне также пользовались не правильной формулой для определения объёма усеченной пирамиды с квадратным основанием, тогда как египтяне знали правильную формулу.
Применительно же ко времени Пифагора (570-490 гг. до н. э.) сложно говорить об иррациональных величинах как таковых, но лишь об открытии иррациональности √ 2. По мнению историков науки, открытие знаменитой теоремы Пифагора стало возможным на основе теории пропорций, его акустическим исследований и математическим открытиям. Пифагору были известны арифметика, геометрия, гармонические пропорции: три средних пропорциональных величины, а также «музыкальная пропорция», непосредственно связанная с его музыкальными экспериментами. Опираясь именно на эти теоретические основания, Пифагор и открыл свою знаменитую теорему.
Если бы Пифагор действительно открыл иррациональность √ 2, то это, безусловно, нашло бы отражение в античной литературе. Однако таких сведений до сих пор не найдено. Если Фалес в отличие от вавилонян и египтян впервые занялся «угловой» геометрией, то Пифагор сделал следующий шаг, положив начало стереометрии, построив такие пространственные формы как правильный тетраэдр и куб. Классическое же доказательства иррациональности √ 2, т.е. несоизмеримости диагонали квадрата с его стороной даётся в приложении к Х книге Евклида.
Тем не менее к какой бы реконструкции первоначального доказательства иррациональности мы не пришли, остается очевидным, что это открытие явилось важнейшим этапом становления не только древнегреческой философии математики. Ибо для математиков и геометров Древней Греции во-первых, был очевиден тот факт, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики и во-вторых, не менее очевидным и значимым был для них факт, что объединяющим началом всех вещей служат численные отношения, выражающие гармонию и порядок природы.
Более того, сама история науки показала, что уже в самой античности теорема Пифагора не только получила громкую известность, но и была осознана как выдающееся достижение теоретического знания, в том числе и в вследствие того, что приводит к появлению иррациональных чисел, являющихся, как и известное всем число π, следствием нарушения диалектического единства качественных и количественных аспектов объектов в классической геометрии.
И именно Пифагору наука обязана одной из своих последующих идей, оплодотворившей развитие как античного, так и современного искусствознания – природа подчиняется скрытым закономерностям, выразимых с помощью математики. Космос, учил Пифагор и вещи в нем суть соразмерное единство противоположностей. Аристотель в «Метафизике» обозначает у пифагорейцев десять таких противоположностей, определяющее место среди которых занимает отношение предела и беспредельного или конечного и бесконечного. В свете такого понимания, мир в целом есть ни предел, ни беспредельное, но предстаёт как единство этих противоположностей, определяющей как космическую гармонию, так и гармонию каждой вещи. Из предела и беспредельного далее возникают числа.
Из чисел создаются геометрические фигуры, порождающие материальные элементы. Числа при этом остаются не хаотическими, а гармоническими. И именно эта числовая гармония и создает гармонически устроенный Космос. По мнению А.Ф. Лосева, сформулированному им во вводной статье к диалогу Платона «Пир», «рассуждения пифагорейцев о пределе и беспредельном далеко не беспредметны и имеют в своей основе попытку отыскать научную закономерность в соотношении этих двух явлений» [1, с. 298].
Одна из двух наиболее многочисленных груп последователей Пифагора – пифагорейцы разработали в геометрии теории параллельных линий, теорему о сумме углов треугольника, четырехугольника и правильных многоугольников. Кроме того, они исследовали окружность, правильные многогранники и шар, открыли правильный пятиугольник и доказали, что плоскость может быть покрыта равносторонними треугольниками, квадратами и шестиугольниками.
При убежденности пифагорейцев в том, что элементы чисел являются элементами всех вещей и весь мир является гармонией и числом, ими было найдено доказательство существования несоизмеримых величин. Оказалось, что для таких элементарных геометрических объектов как диагональ и сторона одного и того же квадрата не существует меры, то есть нет измеряющего их числа. Подобный арифметический вывод практически опрокидывал пифагорейскую философскую систему представлений о Сущем. Попытка преодолеть этот кризис привела к тому, что пифагорейцы стали изучать, в их определении, «неразумные величины», которые мы сегодня именуем иррациональными.
Пытаясь выйти из кризиса, иррациональность отношения диагонали и стороны квадрата пифагорейцы стали объяснять тем, что оба эти отрезка состоят из бесчисленного множества точек и поэтому их отношение сводится к отношению двух бесконечно больших чисел, что в отношении иррациональных чисел в чисто математическом смысле являлось справедливым.
Однако практически в то же время достаточно быстро было обнаружено, что диагональ и сторона квадрата не составляют исключения в возникновении иррациональных чисел. К концу У в. до н.э. математиком и астрономом, пифагорейцем Феодором из Кирены было обнаружено, что стороны квадратов, площади которых равны 3, 5. 6..., 15 несоизмеримы со стороной единичного квадрата т.е. числа √ 3, √ 5, √ 6…√ 15 и далее являются иррациональными соотношениями.
Поскольку же некоторые геометрические объекты не измерялись соотношением целых чисел, пифагорейцам было естественно предположить, что геометрические объекты являются величинами более общей природы. Поэтому в пифагорейской школе была предпринята попытка построить всю математику, основываясь не на арифметике, а на геометрии, в которой все алгебраические операции как записывались, так и разрешались геометрически.
Стали формироваться элементы «геометрической алгебры», которая была заложена пифагорейцами в здание античного учения о формообразовании, где эта идея представлена наиболее рельефно и в котором симметрия была подвергнута наиболее всестороннему анализу. Математическая теория музыки окончательно сформулировала круг родственных дисциплин, которыми занимались в пифагорейской школе – арифметика, геометрия, астрономия и гармония – будущий квадривиум средневековья.
Из пифагорейских математиков, с достоверностью мы знаем одного Гипаса (древн. греч.-Хиппасос из Метапонта, около 450 г. до н.э.),, имена других не сохранились, но это не значит, что их не было, ибо за время жизни Пифагора пифагорейцы достигли в математике слишком многого, чтобы относить все эти достижения только к Гипасу. От Гипаса же проистекала и самостоятельная математическая традиция, нашедшая своё отражение в источнике. УI в. Более того, поздние авторы именно с ним связывают построение вписываемого в шар додекаэдра и собственно открытие иррациональности или несоизмеримых величин.
К концу У в. до н.э. пифагореец Феодор из Киррены (математик и астроном, музыковед и впоследствии учитель Платона) показал, что стороны квадратов, площадь которых равна 3, 5, 6….15, несоизмеримы со стороной единичного квадрата, т.е. числа √ 3, √ 5, √ 6…√ 15 иррациональны, причём он рассматривал каждую иррациональность в отдельности.
Гиппас, который принадлежал к тайному обществу пифагорейцев, обнаружил в своих исследованиях на пятиугольнике, что отношение длины кромки к диагонали не может быть представлено как часть целых чисел. Этот результат противоречил убеждению пифагорейцев в том, что мир может быть полностью описан целыми числами. По иронии судьбы, опровержение этой точки зрения было обнаружено в пентаграмме. Таким образом, Гипас обнаружил явление иррациональных чисел в несоизмеримости маршрутов и два размера, которые пропорциональны так называемому «золотому соотношению», обозначенному впоследствии по первой букве имени греческого скульптора Фидия значением Ф.
Согласно неподтвержденным сообщениям, Гиппас обнародовал свое открытие против правил своего тайного общества публично и поэтому был потоплен как наказание. Первое подробное описание золотого сечения происходит от Евклида (около 300 г. до н.э.), который наткнулся на его исследования так называемых «платоновских тел» или многоугольников, среди них пентагона или пентаграммы.
В истории науки существуют различные гипотезы относительно того почему другой греческий математик – Феодор Киренский (ок. 340 г. до н. э. - ок. 250 г. до н. э.) известный как учитель Платона, а также как персонаж диалогов Платона «Теэтет», «Софист» и др. не смог доказать иррациональность следующего числа √17 и далее. Работа Феодора известна по единственной теореме, которая представлена в литературном контексте трактата «Теэтет» («Theaetetus»), в котором его ученик Театетус приписывает ему теорему о том, что квадратные корни неквадратных чисел до 17 являются иррациональными:
Одна из объяснений основывается на предположении, что ее доказательства Феодора основывались на учении о чётном и нечётном, а первое числе, для которого этот способ не существует, как раз и есть √ 17. Однако уже в начале 1У в. до н.э. одним из учеников Феодора (доподлинно имя неизвестно) было получено общее доказательство иррациональных чисел вида √ N, где N – целое число, не являющееся полным квадратом. Другое возможное объяснение исходит из вероятности того, что Феодор применил так называемый «евклидовов алгоритм», описанный в «Элементах» Евклида как тест на несоизмеримость. В современных терминах теорема состоит в том, что вещественное число с бесконечным продолжением дробных дробей является иррациональным, а иррациональные квадратные корни имеют периодические разложения [2, с.14].
Уже Платон знал, что известная последовательность величин, возрастающая по определенному закону, может быть продолжена в бесконечность и может, как угодно близко подходить к основному пределу, тем не менее, никогда его не достигая. В диалоге «Пир» Платон разделяет вещь и идею вещи и, как отмечал А.Ф. Лосев, Платон использует здесь, по крайней мере, одну великолепную возможность, а именно толкует идею вещи как предел ее становления. Для Пифагора числа были одновременно и источником любой формы, формообразования и оформления. Числа это первая определенность Бытия, еще лишенная какого-либо качества. Числа суть не абстрактные элементы счета, но самостоятельные и объективные субстанции, которые ввиду своей без качественности является чем-то гораздо боле первичным, чем само Бытие и чем даже сами идеи.
В этом смысле числа, в понимании Пифагора, суть сверхсущностные единицы. И лишь вступая в синтез с окружающим их инобытием, наполняются этим инобытием и потому получают качество, образуя собой бытие. Пифагор прямо говорит о том, что все происходит не из числа, но сообразно с числом, ибо в числах присутствует первичная упорядоченность и в исчислениях предмета последовательно упорядочено первое, второе, и т.д. И здесь представляет безусловный интерес, так называемый пифагорейский знак или пентаграмма.
Основное содержание пентаграммы, считавшейся пифагорейским символом – это звездообразный пятиугольник, стороны которого образуют в описанном круге хорды дуг величиной –
В – 4 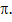
5 Пифагорейский знак был геометрическим символом отношений, характеризующим эти отношения не только в математической, но и в пространственно – протяжённой и структурно-пространственной формах. При этом он принимался за инвариант преобразования геометрической симметрии не только живой, но и неживой природы. В качестве небольшого отступления напомним, что числом Ф и его гомологами характеризуется правильный десятиугольник, шестиконечная «звезда Соломона», и правильный пятиугольник, определяющий очень важный вид симметрии в природе – пентагональную симметрию. Если вершины пятиугольника соединить через одну, получится пятиконечная звезда – фигура, чрезвычайно богатая пропорциями «золотого сечения», символ совершенства и одновременно эмблема пифагорейского ордена.
Правильный пятиугольник и вписанная в него пятиконечная звезда, образующая пентаграмму, которой в истории цивилизации во многих культурах приписывались исключительные магические свойства. Благоговейное отношение к пентаграмме было характерно и для средневековых мистиков, которые в этом плане много заимствовали у пифагорейцев. Именно начиная со средних веков, пентаграмме стали приписывать свойство охранного знака от Сатаны. Достаточно вспомнить в этой связи как описывает Гёте проникновение Мефистофеля в келью доктора Фауста, над входом которой была начертана пентаграмма.
По видимому изначально как знак пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют и пяти-лепестковые цветы плодовых деревьев и кустарников, и морские звезды. И те и другие создания природы человек наблюдал уже тысячи лет. Отсюда естественно предположить, что геометрический образ этих объектов – пентаграмма стала известна в истории цивилизации и культуры раньше, чем «золотая пропорция».
Несколько тысячелетий спустя Леонардо да Винчи в работе «О мощи математики и о количественном изучении явлений» (1508) производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в «золотом делении». Таким образом, было доказано, что звездчатый пятиугольник также обладает «золотым сечением». Примечательно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет константным.
Геометрически меру «золотого сечения» в пятизвездной пентаграмме, которое Евклид называл ещё «непрерывным делением», можно найти несколько раз. Правильный пятиугольник и вписанная в него пятиконечная звезда, образующая пентаграмму, которой в истории цивилизации во многих культурах приписывались исключительные магические свойства.
Мефистофель сначала послал черного пуделя отгрызть кончик двери с записью пентаграммы. Пентаграмма здесь тот самый волшебный знак у порога, который, будучи плохо начертан, дал возможность Мефистофелю войти, но не позволил выйти из комнаты Фауста. При этом критерием, определяющим отношение высоты колонны к длине колоннады, было расстояние между двумя колоннами, являющимися средне пропорциональными значениями. Невзирая на подобные архитектурные подтверждения, следования греками исключительно пропорциональным величинам, существуют веские основания полагать, что «золотая», иррациональная пропорция Пифагору была все же известна.
Пифагорейцы выбрали звездчатый пятиугольник в качестве талисмана. Она считалась символом здоровья и служила опознавательным знаком, но непосредственно как эмблема здоровья была принята лишь в Древней Греции. Косвенным доказательством этому служит существование иррациональных соотношений в греческом строительстве, где господствовали протяженные величины, использование которых может быть обосновано вне прямой связи с мистикой у пифагорейцев дискретных чисел такт как мироощущение греков четко разграничивало геометрически протяженные, а значит, всегда непрерывные величины от дискретных чисел.
Чрезвычайно интересны представления о том, почему же пентаграмма была избрана пифагорейцами в качестве эмблемы их союза. Одно из подобных обоснований исходит из того, что пентаграмма – иначе равнобедренный треугольник, у которого углы при основании = 72º, что вдвое больше угла при вершине 36º, обладает совершенно уникальными свойствами – биссектриса угла при основании делит противоположную сторону в известной пропорции «золотого сечения».
И именно это замечательное свойство пентаграммы была названа в последующем средневековыми математиками, архитекторами и художниками «возвышенным треугольником». А. В. Волошинов математически доказывает, что «…пентаграмма буквально соткана из «золотых пропорций» во всех своих средних значениях» [3, с. 72]. Поэтому не удивительно, что столь редкие математические и геометрические свойства должны были приводить пифагорейцев в восторг.
Необычное пропорциональное строение, красота её внутреннего математического содержания является основанием и красоты её внешней формы, ибо то, что пропорциональное, в представлении пифагорейцев, то, вне сомнения и красиво. К математически- геометрической красоте пентаграммы пифагорейцы присоединяли ещё и суммы женского – 2 и мужского – 3 чисел.
Закономерным следствием математического совершенства этой фигуры, соединением в ней мужского и женского начал явилось то, что пентаграмма воспринималась в пифагорейской школе и как символ жизни и здоровья. В отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин были известны еще в древности, хотя изначально термины «рациональные» и «иррациональные» числа относились не к самим числам, а к несоизмеримым величинам, которые сами пифагорейцы называли «выразимыми» и «невыразимыми», а математики классической эпохи пользовались только рациональными (целыми, дробными и положительными) числами.
Даже в своих «Началах» Евклид излагает учение об иррациональностях исключительно геометрически. Математики же Индии, ближнего и среднего Востока, развивая тригонометрию, алгебру и астрономию не могли обойтись без иррациональных числовых величин (десятичные разложения которых не периодичны и бесконечны), которые, тем не менее, длительное время не признавали за числа. Более развитая в то время вавилонская наука явилась своего рода предтечей и основанием для греческой науки. Достаточно сказать, что теорему Пифагора за 1000 лет до её рождения, правда, только лишь в своих частных прикладных приложениях была начертана на вавилонских глиняных табличках.
А в своих прикладных аспектах теорема Пифагора была обнаружена ещё ранее – в египетском треугольнике, различных задачах и папирусе фараона Аменемхета 1 (ок. 2000 до н.э.), в вавилонских клинописных табличках царя Хамураппи ХУ111 в. до н.э.), в XVI – нач. XVII в. до н.э. в древнейшем китайском трактате «Чжоу-би суань цзин» (математический трактат о гномоне, астрономическом инструменте, позволяющем определить угловую высоту солнца).
В древнеиндийском геометрическо-телеологическом трактате «Сульва-сутра» («Правило верёвки») У11-У в. в. до н.э. вавилонские писцы и жрецы за тысячу лет до Пифагора решали квадратные уравнения, которые хотя и были сформулированы в численном виде и имели характер преимущественно хозяйственных и астрономических задач, но, как свидетельствуют историки науки, явно выходили за пределы того, что определялось в тот период материальной необходимостью [4, с. 39]. Число 2 не является иррациональным; оно может быть записано как частное от деления двух целых чисел: 2/1 = 2. Тем не менее √ 2 является иррациональным.
Если бы это значение было рациональным, оно могло бы быть записано как частное от деления двух целых чисел. Пифагор считал, что все величины в природе можно было бы назвать рациональными числами. Как гласит история, его ученик Гиппасос обнаружил, что √2 является иррациональным. Однако открытие иррациональных чисел, как свидетельствует история философии, было шокирующим для пифагорейцев, и Гиппасос, по преданию, утонул в море, по-видимому, как наказание от богов за разглашение тайны этого открытия.
Пифагор не знал, что значение √ 2 иррационально, так как иррациональность√ 2, как и число π, были доказаны Эйлером в лишь период с 1737 до 1761 гг. Тем не менее Пифагор считал, что все числа, в том числе и рациональные можно записать в виде соотношения и защищал эту позицию довольно яростно. Суждения о том, что существовали числа, которые не могут быть записаны в виде отношения, в то время было недалеки от ереси.
Вавилонская математика и астрономия оставалась вычислительным, но не теоретическим знанием. В 30-х годах ХХ века, когда появилась возможность дешифровки математических табличек вавилонян и возникла возможность ознакомиться непосредственно с их результатами в этой области, обнаружилось, что уровень вавилонской математики был несоизмеримо более высоким, чем последующий уровень египетской.
В то же время рост сведений о египетской математике, в частности, издание знаменитого папируса Ринда, показал очень примитивный характер египетской геометрии, что привело в дальнейшем к более сдержанной оценке историками науки влияния достижений египтян на математику греков и школу Пифагора. В частности и побудило их к поиску истоков греческой науки на Востоке. В Х11 в до н.э. китайцы знали свойство египетского треугольника, а к У1 в до н.э. и общий вид теоремы в древнеиндийском геометрическо-телеологическом трактате «Сульва сутра» («Правило верёвки»).
Как отмечает А. В. Волошинов: «открытие несоизмеримости и обнаружение таких величин, отношение которых не может быть выражено относительно отношения целых чисел явилось главным достижением пифагорейской школы и поворотным этапом в развитии всей математики» [3, с.39]. А по силе революционного воздействия, утверждает там же А.В. Волошинов, «…это открытие, возникшее на рубеже У1-У в.в. до н.э., можно сравнить с открытием дифференциала и интеграла Ньютоном и Лейбницем в начале Х1Х в. или теории относительности А. Эйнштейна в начале ХХ в. «Более того, сама история науки показала, что уже в самой античности эта теорема получила громкую известность и была осознана как выдающееся достижение теоретического знания» [3, с. 144].
Начиная с Х1 книги, в разделах, посвященных стереометрии, Евклидом при построении пространственных тел правильных двенадцати и двадцатиугольников используется известный принцип пропорции, получивший значительно позднее наименовение «золотого сечения» также являющимся несоизмеримым. В 1У и У книгах Евклида этот принцип применяется при построении плоских фигур – правильных пяти и десятиугольников Существо данной пропорции подробно рассматривалось также в космологическом трактате Платона «Тимее».
Сами по себе два члена, утверждал знаток астрономии Тимей, не могут быть хорошо сопряжены без третьего, ибо необходимо, чтобы между одними другим родилась некая объединяющая их связь. «Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепила бы их» Это наилучшим образом может выполнить пропорция или «средняя величина». [4, с. 277]. В этом случае, утверждал Платон, наибольшей степени единства можно достигнуть, если середины находятся в одинаковом отношении к крайним величинам, к тому, что больше и к тому, что меньше, и между ними существует пропорциональная связь.
Если их двух плоскостей нужно составить плоскость, то между крайними величинами (длинами А и С), утверждал Платон, потребуется соединяющая их средняя В, одна и та же для соединяемых плоскостей.Только наличие равной, одинаковой стороны у соединяемых плоскостей принадлежащим одновременно обоим соединяемым телам А и С. позволяет, составив их вместе, получить некое единое целое. Если же нужно получить целое, сплачивая объемы, то здесь требуется уже не одна, а две общие величины, две «середины», принадлежащие одновременно обоим соединяемым телам В и С.
В отличие от Евклида у Платона правильных многогранников всего пять. При этом поверхность последнего из них – додекаэдра, в отличие от четырех остальных, образована фигурой «золотого сечения» – правильным пятиугольником. Платон не строит додекаэдр, но отводит ему совершенно особое место, связывая его со стихией Космоса – «в запасе оставалось еще пятое многогранное построение – его Бог определил для Вселенной и прибегнул к нему, когда разрисовывал её и украшал» [4, с. 242]. Платон с неизбежностью приписывал этому геометрическому построению особый космологический статус, на основе которого у него возникает трехмерный символ Вселенной и достигается целостность геометрического представления о ней.
Поясняя сказанное, позволим здесь небольшое отвлечение. Древние не знали как таковые величины «золотого сечения» при Ф = 1, 618 и Ф = 0,618, но достаточно близко подошли к ним. Древнейшие тексты и историография этого времени свидетельствует о том, что уже вавилоняне пользовались также и иррациональными числами 1,618 и 0,618, но получали данные величины не из математических вычислений, а применяли пропорциональные циркули с различными отношениями между длинами их ножек при строительстве, архитектуре и решении определённых практических задач.
Отсюда следует, что на ранних этапах цивилизации числовая и геометрическая величина «золотого сечения» изначально возникла не как следствие математических изысканий, но вытекала исключительно из решения определённых практических задач с использованием множества весьма нехитрых приспособлений среди которых выделяется применение в архитектуре и строительстве различного рода пропорциональных циркулей.
Примечательно, что в отличие от чертежных циркулей со свободным ходом ножек, пропорциональные циркули, близкие к значениям «золотого сечения», не требовали каких-либо вычислений, позволяя легко строить между собой пропорциональные элементы объекта, допуская при этом свободное пользование любым масштабом. Таким образом, не вызывает сомнений, что Древний Мир широко пользовался не только целыми числами, но, по преимуществу геометрически-иррациональными значениями величин, получаемых из Ö 2 и Ö 3 на основе пропорциональных циркулей.
Для древних греков условием некоего устойчивого совершенства и гармонии являлась необходимость обязательного присутствия пропорциональной связи или, в понимании Платона, «согласного строя». И именно эти убеждения и геометрические знания были положены в основу античной архитектуры и искусства.
Например, при выборе основных размеров греческого храма критерием высоты и глубины служила его ширина, которая являлась средне пропорциональной величиной между этими размерами. Точно так же реализовывалась связь между диаметром колонн и их высотой. При этом критерием, определяющим отношение высоты колонны к длине колоннады, было расстояние между двумя колоннами, являющимися средне-пропорциональными значениями.
Древними греки узнали большую часть своих знаний о священной архитектуре и сокральных пропорциях в архитектуре строительстве от египтян, поэтому не удивительно, что в Парфеноне и других греческих храмах мы находим использование практически одинакового набора пропорций. Парфенон был спроектирован и построен таким образом, что заключал в себе несколько геометрических пропорций, близких по значению к числу «золотого сечения», хотя его использование особенно заметно в пропорциях, очерченных его фасадом.
Невзирая на подобные архитектурные подтверждения, следования греками исключительно пропорциональным величинам, существуют веские основания полагать, что «золотая» или иррациональная пропорция Пифагору была все же известна. Косвенным доказательством этому служит существование иррациональных соотношений в греческом строительстве и архитектуре где господствовали протяженные величины, использование которых может быть обосновано вне прямой связи с мистикой у пифагорейцев дискретных чисел так как мироощущение (ментальность) греков четко разграничивало геометрически протяженные, а значит, всегда непрерывные величины от дискретных чисел.
Древними греки узнали большую часть своих знаний о священной архитектуре и сокральных пропорциях в архитектуре строительстве от египтян, поэтому не удивительно, что в Парфеноне и других греческих храмах мы находим использование практически одинакового набора пропорций. Парфенон был спроектирован и построен таким образом, что заключал в себе несколько геометрических пропорций, близких по значению к числу «золотого сечения», хотя его использование особенно заметно в пропорциях, очерченных его фасадом.
В частности, если высота конструкции от его основания до пика равна единице, то ширина структуры по фасаду составляет ровно 1,618. Как и в случае с храмом Рамсеса в Египте, размещение столбов и многих других сторон здания также определяются экспоненциальными факторами «золотой пропорции».
Однако, для того, чтобы получить некоторые гармонические отношения близкие к значению «золотого сечения», данные пропорциональные отношения с закономерной неизбежностью и последовательностью должны были стремиться к максимальному количеству отмеряемых таким образом геометрических величин и отрезков, чтобы композиция, скажем, архитектурного объекта имела не отдельные пропорции «золотого сечения», а целые пропорциональные ряды.
Так, например, из вычислений Б. Смоляка пропорций Парфенона следует, что если принять за единицу ширину торцового фасада храма значение Ф, то мы получим ряд золотого сечения из 8 членов 1: Ф1 : Ф2 : Ф3 : Ф5 : Ф8 : Ф13……, где Ф = 0,618
[5, с. 253]. Их геометрическая, числовая особенности и строение пропорциональных циркулейсостоит в том, что ось вращения лежит в средней части обеих ножек, позволяя получать различные меры или кооффициенты пропорциональности. При каждом раскрытии угла циркуля возникает два размера или две меры – из них малая мера представляет собой расстояние между остриями малых ножек, а большая мера – расстояние между остриями больших плечами ножек.
Геометрическая и числовая особенность и строение пропорциональных циркулей, состоит в том, что ось вращения лежит в средней части обеих ножек, позволяя получать различные меры или кооффициэнты пропорциональности. При каждом раскрытии угла циркуля возникает два размера или две меры – из них малая мера представляет собой расстояние между остриями малых ножек, а большая мера – расстояние между остриями больших плеч ножек.
Вполне допустима гипотеза, что данная конструктивная их особенность и явилась собственно основанием для открытия древними зодчими пропорции «золотого сечения» при решении практических задач на деление отрезка на две части с их использованием. Не менее вероятно и предположение, что это могло произойти всего лишь после нескольких попыток их применения.
«Золотая пропорция» в искусстве Древнего мира, как известно, встречается во многих произведениях – помимо здания Парфенона, в усыпальнице Тутанхомона, терракотовых изделиях этруссков, храме Зевса в Олимпии, скульптурах Фидия мн. др. Так, например, хорошо известна созданная из чистого золота в 1300 г. до н.э маска Тутанхомона в пропорциональном отношении содержит пятиугольную симметрию, содержащую внутри себя целый ряд пропорций «золотого сечения». И хотя многие видели этот довольно популяризированный образ, его очевидная пятиугольная пропорциональность редко упоминается или представлена в научной литературе.
В то же время использование пропорции «золотого сечения» в этом случае является вполне закономерным, ибо египтяне полагали, что помещение мумии в храм являлось основанием для последующего возрождения посвященного к новой жизни – профанальная личность умерла, а духовный человек рождался после его смерти. Регенеративный тип возрождения и, следовательно «золотая пропорция», играла очевидную роль в идее возрождения фараонов в течение всей жизни. Поэтому подобную геометрическую форму можно найти в многих египетских постройках, в часности, в строениях мегалитического комплекса Осириона.
И хотя Евклид, предположительно, и определил математическое значение «золотого сечения» около 300 г. до н.э., а последователи Пифагора, вероятно, знали об этом и два века спустя, трехтомный трактат Лука Пачоли «Божественная пропорция», написанный в эпоху Возрождения имел решающее значение для распространения «золотого отношения» за пределами мира математики в области архитектуры, скульптуры, живописи и далее, во времена Средневековья, когда большая часть знаний, полученных более ранними греческими и римскими культурами были утрачены и в Европе в целом мало интересовались восстановлением древних знаний.
Поскольку письменных материалов, переживших темные годы между падением Рима, Средневековьем и эпохой Возрождения сохранилось крайне мало те, кто интересовался древними культурами, были вынуждены обратиться к изучению руин и реликвий, которые они оставили.
Помимо гармонических размеров теоретики эпохи Возрождения использовали и иррациональные пропорциональные отношения. Так, например использование иррациональных гармонических пропорций связанных с числом Ф, можно найти на фреске «Скаола ди Атене» (Афинская школа) Рафаэля, которую можно представить и в форме описание рациональных гармонических числовых пропорций в соответствии с пифагорейским пространством тангажа, а также иррациональным «золотым соотношением», воплощённным как программа пропорциональной структуры фресок. Помимо трактата Пачоли наличие «золотого сечения» можно найти также в практических работах архитектора Возрождения Джакомо да Виньолы.
Такие скрипичные мастера как Гварнери, Страдивари, Маджини применяли построения «золотой пропорции», как правило пятиугольник или пентаграмму при изготовлени своих скрипок [6, с. 144]. Более поздний пример архитектурного стиля, известного как стиль барокко, процветавшим в ХУ11 веке известен своими весьма сложными и нерегулярными формами, однако, использование пятиугольной симметрии по-прежнему было широко распространено, хотя его воплощение можно было бы назвать скорее нерегулярным и не столь очевидным.
И. Кеплер назвал «золотую пропорцию» продолжающей саму себя, устроенную так, что что два младших члена этой нескончаемой пропорции в целом дают третий член, причём та же пропорция сохраняется до бесконечности [7, с.72]. В последующие века «золотая пропорция» превратилась в искусстве в академический канон. Причём построение ряда отрезков, как оказалось, можно было производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд). Фундаментальное значение числа Ф, его «основополагающий» характер дают основание приобщитть его к двум другим фундаментальным значениям, лежащем воснове мироздания – числу π, выражающему отношение длины окружности к её диаметру и «е» – основанию натуральных логарифмов.
Характерно, что все эти три числа являются несоизмеримыми, символизирующими единство непрерывного и дискретного. Таким образом новые системы исчисления с иррациональными числами как бы ставят «с ног на голову» сложившуюся систему иерархи отношений между рациональными и иррациональными числами, которые появились только после открытия пифагорейцами несоизмеримых отрезков.
В дальнейшем учёные продолжали активно развивать теорию чисел Фибоначчи, выражающей прогрессию «золотой пропорци», Так, например Ю. Матиясевич с использованием её чисел решает 10-ю теорему Гилберта, возникают изящные методы решеничя ряда кибернетических задач. На основе кодов «золотой пропорции» можно выразить либо действительное число в виде суммы степеней «золотой пропорции» с целым коофициэнтом. Принципиальное отличие полдобного способа кодирования чисел состоит в том, что основания новых кодов также представляют собой «золотую пропорцию» и также оказываются иррациональными числами.
Согласно современным представлениям «золотая пропорция» представляет собой ассиметричную симметрию в науках о пропорциях. Прежде всего в архитектуре, строительстве, живописи и т.д., проявляющейся в статистической и динамической симметрии. Статистической симметрии свойственны равные отрезки и величины, для динамической симметрии харакетрно увеличение или уменьшение отрезков Выражающих величины «золотой пропорции» возрастающего или убывающего ряда
[8, с.154]. Числовое значение «золотого сечения» относится к иррациональным числам и представлено целыми числами, такими, например как 1, 2 и т. д. При этом существенным является то их свойство, что все иррациональные числа не все в равной мере иррациональны. Иными словами. некоторые иррациональные значения будут более иррациональны, чем другие.
Причём если рассматривать меру иррациональности в той степени, в которой ее можно приблизить к этому иррациональному числу, скажем, к числу «золотого сечения» с помощью рациональных чисел, то можно увидеть существование различных уровней иррациональности, в которой в существующей прогрессии иррациональных чисел «золотое число» Ф, отражающее буквенное обозначение «золотого сечения» является и самым иррациональным из всех иррациональных чисел. Подобное его особенность может показаться нам необычной, так как пропорция «золотого сечения», равная 1,618 помимо того, что является наиболее нерациональной, в то же время является и самой гармоничной числовой и геомерической пропорцией.
Объяснение этой его характеристики состоит в том, что это пропорциональное отношение является не только противоположностью рационального, но и в числовом отношении находится на максимальном расстоянии до него. Более того этом его качественной характеристике сталкиваются такие, казалось бы, непримиримые и противоречивые значения как рациональность и иррациональность, хаос и красота.
Таким образом, по-видимому числовое соотношение Ф играет особую роль в согласии противоположностей. Подтверждением этому является известный нам из теории фракталов факт, что приближённые иррациональные значения могут быть обнаружены в беспорядке, которые, также является и выражением пропорциональных связей. Как оказалось, И Беспорядок и Хаос также могут составлять пропорциональные объекты, которые мы можем воспринимать как обладающими эстетическими характеристиками и как безусловно красивые.
Открытие «несоизмеримых отрезков» привело также к первому кризису в основаниях математики и стало поворотным пунктом в ее развитии [9, с. 14]. Для преодоления этого кризиса выдающийся геометр Евдокс Книдский (ок. 355 г. д. до н.э.) предложил, так называемый, «метод исчерпывания» с помощью которого он преодолел указанный кризис. Считается, что данная теория предвосхитила современную «теорию измерений» и теорию «иррациональных чисел», построенную немецким математиком Рихардом Дедекиндом только в Х1Х столетии [10, с. 27].
И всё же, к какой бы реконструкции первоначального доказательства иррациональности мы не пришли, остается очевидным, что это открытие явилось важнейшим этапом становления не только древнегреческой математики философии. Не случайно, видимо, по словам известного современного математика М. Клайна (1993), «то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки.
Во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики, во-вторых, что объединяющим началом всех вещей служат численные отношения, выражающие гармонию и порядок природы
[9, с. 136]. Представляется, однако, что общее значение открытия несоизмеримых отрезков и иррациональности для развития и математики, философии, искусства и науки в целом не исчерпывается указанными последствиями, хотя внешне, безусловно, выражается, прежде всего, в них.
Итак, отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин были известны еще в древности, хотя изначально термины «рациональные» и «иррациональные» числа относились не к самим числам, а к несоизмеримым величинам, которые сами пифагорейцы называли выразимыми и невыразимыми, а математики классической эпохи пользовались только рациональными (целыми, дробными и положительными) числами.
Открытие несоизмеримости впервые, быть может, заставило рождающуюся греческую науку сознательно задуматься о своих предпосылках. Ведь такие понятия как числа, точки, фигуры и т. д., которыми оперировали пифагорейцы изначально, еще не были логически прояснены и продуманы. Именно в этом, кстати, упрекают пифагорейцев и Платон, и еще больше Аристотель. В самом деле, говорил Аристотель, числа у них не отделены от вещей. В тоже время нельзя и сказать, чтобы числа у них сознательно и обоснованно отождествлялись с вещами. Вопрос об онтологическом статусе чисел в этом плане просто не возникал, а потому здесь и царила некоторая не прояснёность и не определённость.
Открытие несоизмеримости стало также и первым толчком к осознанию оснований философско-математического исследования, к попытке не только найти новые методы работы с величинами, но и понять, что такое величина. Как следствие это осознания – основу последующего философского учения пифагорейцев составила категориальная пара двух противоположностей – предела и беспредельного.
«Беспредельное» не может быть единым началом вещей, иначе ничто определённое, никакой «предел» не был бы мыслим. С другой стороны, и «предел» предполагает нечто такое, что определяется им. Отсюда следовал вывод Филолая о том, что «природа, сущая в космосе, гармонически сложена из беспредельных и определяющих величин – «так устроен и весь космос, и все, что в нём». Открытие «несоизмеримых отрезков» привело также к первому кризису в основаниях математики и стало поворотным пунктом в ее развитии.
В этой связи, не лишне напомнить, что одним из ее результатов являются так называемые «аксиомы непрерывности», на которых основывается другое достижение математики – «абстракция актуальной бесконечности», введенная также немецким математиком Георгом Кантором (1845-1919) в его «теории бесконечных множеств» с указанием на возможность бесконечной длительности процесса измерения с неизбежным появлением иррационального числа и доказательством реальности этой ситуации. Это привело к нарушению тезиса Аристотеля о невозможности существования актуальных бесконечных объектов, очередному кризису в математике и как вынужденное следствие – созданию «конструктивной математики» (А. А. Марков – 1972), основанной на использовании более скромного представлении о бесконечности, называемой «потенциальной бесконечностью» [11, с.17].
В отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин были известны еще в древности, хотя изначально термины «рациональные» и «иррациональные» числа относились не к самим числам, а к несоизмеримым величинам, которые сами пифагорейцы называли выразимыми и невыразимыми, а математики классической эпохи пользовались только рациональными (целыми, дробными и положительными) числами.
Открытия иррациональности во времена Пифагора привело к теоретической нестабильности большей части геометрии пифагорейцев, которые основывались на несовершенной теории пропорций, применявшихся только к числам. Поэтому открытие несоизмеримости в то время должно было потребовать большой переделки всей ткани элементарной геометрии в ожидании открытия общей теории пропорций, применимой как к несоизмеримым, а также к соизмеримым величинам.
В то же время открытие иррациональных чисел вызвало первый кризис в математике. Оказалось, что в прямоугольном треугольнике ни из какой, сколь угодно малой части катета, невозможно сложить гипотенузу: они несоизмеримы, несопоставимы в то время как пифагорейцы знали лишь целые сакральные числа.
С иррациональными числам греческие математики сумели совладать лишь в 111 веке до н.э. Произошла частичная десакрализация математики пифагорейцев, открывшая уникальную возможность задуматься об основаниях этой дисциплины и наметить новые пути её развития. В то же время, как отмечает А.В. Волошинов, «открытие несоизмеримости и обнаружение таких величин, отношение которых не может быть выражено относительно отношения целых чисел явилось главным достижением пифагорейской школы и поворотным этапом в развитии всей математики» [12, с.140]. А по силе революционного воздействия, утверждает там же А. В. Волошинов, это открытие, возникшее на рубеже У1-У в.в. до н.э. можно сравнить с открытием дифференциала и интеграла Ньютоном и Лейбницем в начале Х1Х в. или теории относительности А. Эйнштейна в начале ХХ в.
Математическая теория музыки, которую в то же время можно рассматривать и как античную музыкальную эстетику окончательно сформулировала круг родственных дисциплин, которыми занимались в пифагорейской школе – арифметика, геометрия, астрономия и гармония – будущий квадривиум средневековья. Применительно же ко времени Пифагора вообще нельзя говорить об иррациональных величинах, но лишь об открытии иррациональности √ 2. По мнению историков науки, открытие знаменитой теоремы Пифагора стало возможным на основе теории пропорций, его акустических исследований и математическим открытиям.
Пифагору были известны арифметика, геометрия, гармонические пропорции и три средних пропорциональных величины, а также «музыкальная пропорция», непосредственно связанная с его музыкальными экспериментами. Опираясь именно на эти теоретические основания, он и открыл свою знаменитую теорему. Если бы Пифагор действительно открыл иррациональность √ 2, это, безусловно, нашло бы отражение в античной литературе. Однако таких сведений до сих пор не найдено.
Если Фалес в отличие от вавилонян и египтян впервые занялся «угловой» геометрией, то Пифагор сделал следующий шаг, положив начало стереометрии, построив такие пространственные формы как правильный тетраэдр и куб. Классическое же доказательства иррациональности √ 2, т.е. несоизмеримости диагонали квадрата с его стороной дается в приложении к Х книге Евклида.
Однако к какой бы реконструкции первоначального доказательства иррациональности мы не пришли, остается очевидным, что это открытие явилось важнейшим этапом становления не только древнегреческой математики философии. Не случайно, видимо, по словам известного современного математика М. Клайна (1993), то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции, пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки. Во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики, во-вторых, что объединяющим началом всех вещей служат численные отношения, выражающие гармонию и порядок природы.
Представляется, однако, что общее значение открытия несоизмеримых отрезков и иррациональности для развития и математики, искусства и науки в целом не исчерпывается указанными последствиями, хотя внешне выражается, прежде всего, в них. Это открытие впервые, быть может, заставило рождающуюся греческую науку сознательно задуматься о своих предпосылках.
Открытие несоизмеримости стало первым толчком к осознанию оснований философско-математического исследования, к попытке не только найти новые методы работы с величинами, но и понять, что такое величина. Как следствие это осознания основу последующего философского учения пифагорейцев составила категориальная пара двух противоположностей – предела и беспредельного.
Значение открытия несоизмеримости в исории философии состоит не только в том, что нарушило философскую систему пифагорейцев, но и в последующем привело к созданию новых, весьма тонких и глубоких теорий в истории науки, культуре, объектах архитектуры и искусства с использованием иррациональных пропорций и величин. Кризис, возникший в пифагорейской школе, состоявшийся в открытии несоизмеримых отрезков, суть которого состояла в невозможности выразить в рациональных числах, с которыми только и имели дело пифагорейцы диагональ квадрата со стороной равной единице стал для античной философии и математики повортным пунктом в истории, ибо нарушал существующую гармонию между арифметикой и геометрией, гармонию пифагорейской модели мира.
«Осознав, что совокупность геометрических величин представляет собой скорее некое числовое поле, чем простое геометрическое множество или множество рациональных чисел, пифагорейцы создали исчисление в геометрической форме, получившее впоследствии в науке наименование «геометрической алгебры», воссоздав нарушеную было гармонию мира» [13, с.578]. Открытие в пифагорейской школе «несоизмеримых величин», подготовило также переход от количественного к субстанциональному пониманию бесконечности как некой живой характеристики и внутреннних и внешних процессов в мире» [14, с. 136].
По существу одна из важнейших концепций священной геометрии пифагорейцев получила свою преемственность от пифагорейского сообщества через корпорации средневековых строителей в тайные общества Европы ХУ111 века. Как отмечает румынский математик, историк и философ М. К. Гыка в работе «Золотое число: пифагорейские обряды и ритмы в развитии западной цивилизации» (2016), секреты «золотой пропорции» в последующем развитии цивилизации были реализованы не только как основополагающие пропорции в архитектуре, живописи и музыке, но также и как своего рода путь в направлении более глубокого понимания духовной природы красоты и скрытых гармоний, объединяющих все Сущее.
А «универсальность иррациональных величин «золотой пропорции» и их широкое распространение в различных закономерностях и сферах человеческого бытия от науки до культуры, архитектуры и искусства и поныне стимулируют поиски значений, которые объединяли бы их в некую общую теорию, обобщающую и выражающую структуру мировых констант» [15, с. 24, 18, с.398, 22, с.324].
References
1. Losev A.F. Antichnaya estetika (v 8 tomakh).T. 1. Rannyaya klassika.M.: 2001. 624 s.
2. Tatarkevich V. Istoriya filosofii. Antichnaya i srednevekovaya filosofiya. Izd-vo Permskogo universiteta. Per. s pol'skogo V.N. Kvaskova. Perm': 2000, S. 14.
3. Voloshinov A. V. Matematika i iskusstvo M.: Prosveshchenie. 2000. – 400 s.
4. Platon. Sochineniya v trekh tomakh. T.2. M.: 1971. 513 s.
5. Smolyak B. P. O prirode zolotogo secheniya // Arkhitektura SSSR. 1965. № 3. S. 250-261.
6. Shevelev I. Sh., M. A. Marutaev M. A., Shmelev I. P. Zolotoe sechenie: Tri vzglyada na prirodu garmonii. M.: Stroiizdat, 2007. – 343 s.
7. Kepler I. O shestiugol'nykh snezhinkakh. Per. s lat. Yu.A. Danilova. M., «Nauka». 1982 – 194 s.
8. Khembidzh Dzh. Dinamicheskaya simmetriya v arkhitekture. Perevod s angliiskogo V.Belyustina. M. Izdatel'stvo Vsesoyuznoi akademii arkhitektury, 1936. – 202 s.
9. Klain Moris Matematika. Utrata opredelennosti. M.: Mir. 2007. – 640 s.
10. Dedekind, R. Nepreryvnost' i irratsional'nye chisla = Stetigkeit und irrationale Zahlen. 4-e ispravlennoe izdanie. Odessa: Mathesis, 1923. – 40 s.
11. Markov A. A. O logike konstruktivnoi matematiki. (Ser.: Matematika i kibernetika. № 8. M.: Znanie, 1972. – 48 s.
12. Voloshinov A. V. Soyuz istiny, dobra i krasoty. M.: 2017. – 224 s.
13. Tatarkevich V. Istoriya filosofii. Antichnaya i srednevekovaya filosofiya. Izd-vo Permskogo universiteta. Per. s pol'skogo V. N. Kvaskova. Perm'.: 2000. – 482 s.
14. Brunov N. I. Proportsii antichnoi i srednevekovoi arkhitektury. M.: 1936. 140 s.
15. Matila C. Ghyka The Golden Number: Pythagorean Rites and Rhythms in the Development of Western Civilization. Rochester. 2016. – 448 s.
16. Zhmud' L. Ya. Pifagor i ego shkola. L.: Nauka. 2012. – 192 s.
17. Vygodskii M.Ya. Arifmetika i algebra v drevnem mire.-M.: Nauka, 1967.
18. Voloshinov A. V. Soyuz istiny, dobra i krasoty. M.: 2017. – 224 s.
19. Arakelyan G. B. Matematika i istoriya zolotogo secheniya. M.: Logos, 2014. – 404 s.
20. Vasyutinskii N. A. Zolotaya proportsiya. Spb.: Izd-vo «Dilya». 2006. – 202.
21. Stakhov A. P. Kody zolotoi proportsii. Izd-vo «Kniga po trebovaniyu». M.: 2012. – 152 s.
22. Shevelev I.Sh., Marutaev M.A., Shmelev I.P. Zolotoe sechenie. M.: Stroiizdat, 1990. – 343 s.
Link to this article
You can simply select and copy link from below text field.
|
|





