Key of David (on Solution of David Hilbert's Second Problem

Kleschev Denis Sergeevich journalist at "Alapayevsk newspaper" 624603, Russia, g. Alapaevsk, ul. Revolyutsii, 4 nirvansky@mail.ru Other publications by this author

Существуют четыре главные препятствия, которые встают на пути философа и редко когда позволяют ему обрести славное имя истинного мудреца. Препятствия эти суть: первое — следование примеру ненадежного или надуманного авторитета; второе — потворство устойчивым предрассудкам; третье — страх перед осуждением со стороны невежественной толпы; и четвертое — сокрытие собственного невежества под видимостью мудрости.

Роджер Бэкон

AB INITIO

На протяжении всего XX века математика медленно, но неуклонно превращалась из строгой науки в инструмент насилия над человеческим разумом, над самой способностью человека выносить какие бы то ни было суждения. Плачевный итог развития математической науки был подведен в монографии Морриса Клайна «Математика. Утрата определенности» ^{[1, С.354-357]}. Вывод, к которому пришел выдающийся математик и историк науки, неутешительный: несмотря на кажущуюся успешность различных дисциплин, направлений и школ, математика как единая наука прекратила свое существование. Такой же неутешительный диагноз ставит в своей монографии отечественный исследователь оснований математики В.Я. Перминов: «Критика традиционного образа математики приобрела сегодня всеобщий характер и сделалась почти модой. Философы, логики, историки математики и сами математики говорят о нестрогости математических доказательств, о ненадежности интуиции и о принципиальной неустранимости противоречий в фундаментальных математических теориях. Традиционный идеал математики как строгой науки сегодня, как кажется, полностью отвергнут» ^{[2, С.5]}.

Подобно тому, как в триптихе Иеронима Босха «Сад земных наслаждений» первозданный рай, в котором обитают Адам и Ева, где цветет древо жизни и древо познания, ведет в мир игры со стихиями и силами природы, в царство земных наслаждений, плотских утех, необузданного полета фантазии, за которым вдруг наступает картина безумия, инфернальной деградации и смерти всего живого, математическая наука прошла через три длительные стадии — зарождения, расцвета и упадка. Переход из одной стадии в другую был обусловлен тремя глубокими потрясениями или кризисами в основаниях математики, в чем единодушно сходятся все историки науки: кризис античной математики, связанный с открытием несоизмеримых отрезков, кризис новоевропейской математики, связанный с применением бесконечно малых величин и кризис постмодернистской математики, связанный с введением актуальной бесконечности и обнаружением логических антиномий. Причем, как следует из результатов, полученных К. Геделем, никакого выхода из последнего кризиса в рамках стандартной математики не существует. Поскольку, если в ней и содержатся фундаментальные противоречия, то обнаружить их в рамках сложившейся системы аксиом не представляется возможным.

Однако вердикт К. Геделя не является поводом для того, чтобы поддаваться декадентскому настроению философов, перешедших на позиции абсолютного агностицизма и отрицания математической истины. Вывод о том, что доказать непротиворечивость системы аксиом арифметики невозможно, что можно доказать лишь существование в ней противоречий, является лишь первым, самым трудным и самым важным шагом к философскому переосмыслению того чем в действительности является язык математики. Является ли он только искусственным продуктом, плодом человеческого интеллекта, как об этом твердят математики-формалисты, либо подлинные корни этого языка, с помощью которого физики описывают законы материи, а логики — внутренние законы мышления, лежат выше всякой конечной формы, которая может быть выведена человеком.

Невозможность доказать отсутствие противоречий в аксиомах арифметики есть удар, прежде всего, по философии формализма, за которой скрывается непомерное тщеславие европейского человека, решившего присвоить своему имени все законы бытия, мышления, и даже саму бесконечность — тот самый важный математический «объект», который оставалось отловить, засушить и выставить на всеобщее обозрение в трофейной комнате научного позитивизма. Тем не менее, грандиозная программа полной формализации математического языка потерпела крах, но вовсе не потому, что формалисты оказались плохими математиками. Как раз наоборот, их вера в возможность формализации всего и вся, сделала из них превосходных ученых и весьма утонченных мыслителей.

Но бесконечность оказалась не тем «объектом», который может себе присвоить человек, даже если этот человек снабжен самыми совершенными орудиями познания. Титанические усилия, приложенные Г. Кантором и его последователями для того, чтобы «уничтожить» или «оконечить» бесконечность с самого начала были обречены на провал. Так же, как усилия по «уничтожению» бесконечно малых величин, так же, как попытка изгнания из математики иррациональных чисел, предпринятая пифагорейцами. Если внимательно присмотреться ко всем тем кризисам, которые терзали математику на протяжении многих тысяч лет, то окажется, что в них проявляется одна общая черта, а именно стремление подогнать бесконечность под то наивное представление о математическом языке, в котором человек выступает единственным и главным творцом науки, как если бы до изобретения колеса нигде не существовало круговых траекторий и сферических поверхностей, а до открытия Платоновых тел или чисел Фибоначчи не существовало ни кристаллов, ни всего многообразия живой природы.

Сколь бы странным ни показался такой подход, но idea fixa формализма состоит как раз в том, что создателем математики являются исключительно сами формалисты, которые ради удобства выполнения тех или иных операций могут ввести какие угодно аксиомы, создать какие угодно абстракции, ничуть не заботясь о том, как эти абстракции соотносятся с другими областями знаний и совершенно не размышляя об их содержании. Для того, чтобы зачислить созданные человеком абстракции в разряд истины, они должны всего лишь соответствовать формальным правилам того или иного математического диалекта. Такое определение сущности математики как синтетического языка, правила которого зависят лишь от субъекта познания, ведет к быстрому накоплению математических результатов, позволяет разнообразить методы исследования, но в нем содержится опасность появления субъективных ошибок. Такая опасность исходит из постепенного смешения диалектов и построения на их основе других правил и языков, когда некоторое слово, взятое из одного специфического диалекта, становится общеупотребительным без перевода и осмысления его этимологии.

Не задумываясь над тем что обозначалось данным словом, как, для чего и в какой области оно возникло, его начинают использовать в других диалектах, не подозревая даже о том, что смысл одного и того же слова в различных языках претерпевает неизбежные изменения, а в некоторых случаях с ним происходят поразительные трансформации.

Какая, на первый взгляд, разница — запишем мы слово «deus» латинскими буквами или кириллицей, разве может от этого измениться смысл понятия «бог»? Оказывается, может. Ведь, если проделать то же самое с санскритским понятием «бог» — «deva», то мы получим «дева», и тогда без вразумительного контекста станет уже непонятно идет речь о «боге», о «девушке» или о «богородице». В древнеиранской или авестийской традиции «девами» называли не богов, а злых духов, которых мы бы назвали греческим словом «демоны», хотя сами древние греки словом «демоны» зачастую называли «богов». Переписав и прочитав англо-сакское «devil» в знаках деванагари — «devil» вместо «дьявола» мы получим нечто относящееся к «богине». Так, всего несколько строк текста перенесли нас с одного континента на другой сквозь тысячи лет истории и стали причиной неопределенности в понятиях, которыми мы, между прочим, каким-то образом изъясняемся.

С чем-то подобным мы сталкиваемся в математике. В различных ее направлениях и разделах, в привычных для нас словах «чистой математики», таких как «число», «ноль», «единица», «квадрат», «куб», смешаны многие смыслы и представления, возникавшие у мыслителей разных эпох. Однако математики-формалисты не придают этому существенного значения. Для них математические термины существуют в идеальном мире, создателем которого стал человек, очистивший его от возможности появления противоречий путем отречения от всякого рода «неточных» домыслов, в мире, где все слова, формулы, теоремы обитают в неизменном виде, так что даже само время стало не властно над ними. Если интуиционист на вопрос «Где следует искать подлинную математическую точность?» ответит: «в самом человеческом разуме», то формалист без малейшего колебания ответит: «на бумаге» ^{[3, P.81]}.

Таким образом, из формалистского представления о математике была исключена возможность того, что само время тоже может выступать соучастником творческого процесса, что человек, снабженный орудиями познания, есть не только и не столько творец математической истины, сколько средство для ее проявления. То единственное, благодаря чему мы различаем слова и понятия, благодаря чему не сбиваемся в переплетениях мыслей, лежит в области интуиции, а не в области формализма. Как бы ни пытались формалисты найти точность в типографских символах, лишь интуиция устанавливает внутреннюю связь между словами. Для нее нет ничего невозможного в том, чтобы обозреть за формой слов сколь угодно большие промежутки времени и отыскать в них то единственное этимологическое значение, которое не приводит к двусмысленности.

Математика как единая, лишенная противоречий наука не может быть построена без математической интуиции, ведь разрешение возникающих во множественности противоречий и есть одна из основных задач любого из видов интуиции. Только она позволяет мыслить непрерывное (геомертию) и дискретное (арифметику) как диалекты одного языка: «Поскольку значительная часть математики может быть построена на основе арифметики натуральных чисел, порождаемых интуицией времени, то отсуда следует, что "априорность времени не только определяет свойства арифметики как априорные синтетические суждения, но играет ту же роль по отношению к свойствам геометрии"» ^{[4, С.48]}.

Однако именно время выпало из поля зрения формалиcтов, увлеченных идеей полной формализации математики, которая потребовалась им для того, чтобы подогнать бесконечность под введенные Г. Кантором символы. Стремление во что бы то ни стало отловить «объект» (бесконечность) привело к установлению монопольного права формалистов на то что следует называть математикой. История математики оказалась в таком забвении, что произошла невольная фальсификация ряда ключевых моментов ее формирования, ведь многие великие математики прошлого выступали категорически против «оконеченной» или актуальной бесконечности Г. Кантора.

Привычные для школы формализма двойные стандарты были подвергнуты справедливой критике И. Лакатоса, который отмечал, что «формализм отделяет историю математики от философии математики, так как согласно формалистскому пониманию математики, собственно говоря, истории математики не существует (...) Формализм отрицает статус математики для большей части всего того, что некогда понималось как входящее в математику, и ничего не может сказать об ее "развитии". Ни один из "творческих" или "критических" периодов существования математических теорий не может быть допущен в формалистическое небо, где математические теории пребывают как серафимы, очищенные от всех пятен земной недостоверности. Однако формалисты обычно оставляют открытым небольшой черный ход для падших ангелов, если для каких-нибудь "смесей математики с чем-то другим" посчастливится построить формальные системы, "которые в некотором смысле позволяют их туда включить"» ^{[5, С.6]}.

С тех пор, как человек стал присваивать своему имени язык математики, на что в древних цивилизациях налагалось строжайшее табу, с тех пор, как человек решил взять на себя функцию математического бога, наука достигла больших высот, но через «черный ход» в математику проникло немало «падших ангелов». Некоторые из них были изгнаны обратно в преисподнею, некоторые продолжают обитать в стандартной математике, выстроив вокруг себя неприступные стены, прикрываясь авторитетом выдающихся математиков. И только погружение в историю математики или в этимологию ее терминов может оказать помощь в деле их выявления и устранения.

Выдающемуся математику XX века А. Пуанкаре принадлежит замечательная мысль о том, что развитие математики и появление более совершенных теорий можно уподобить эволюционному развитию живых существ. Каким бы совершенным ни был вид организма, в эмбриональной стадии своего развития он всегда повторяет «всю историю его предков в течение геологического времени. По-видимому, то же самое происходит и в развитии ума... По этой причине история науки должна быть нашим первым руководителем» ^{[5, С.10]}. Поэтому негласный запрет формалистов на изучение истории математики и попытки ее искажения можно понимать как стремление к тому, чтобы уничтожить в зародыше появление на свет новых конкурирующих теорий, расширяющих наши знания, как стремление остановить эволюцию самого разума.

IPSE DIXIT

Теорема о сумме квадратов катетов равных квадрату гипотенузы прямоугольного треугольника, известная нам как теорема Пифагора, применялась за тысячи лет до того, как великий древнегреческий философ в VI в до н.э. нашел один из способов ее доказательства. Религиозно-синкретичный характер древнейшей математики, астрономии и архитектуры, а также ограниченный набор сохранившихся текстов не позволяет произвести вполне удовлетворительную датировку события, когда данная математическая закономерность стала известна человеку.

Если опираться на тексты глиняных табличек шумеро-вавилонской культуры, то можно говорить о том, что эта теорема, выраженная в клинописных знаках, была известна уже в древневавилонском царстве (II тысячелетие до н.э.) ^{[6, С.103]}. С другой стороны, исходя из этого, можно впасть в обычную формальную ошибку, отказав древним египтянам в знании оной же теоремы в III или IV тысячелетии до н.э. лишь по причине того, что папирусная бумага выступает менее надежным носителем информации, чем глиняные таблички. В рамках позитивной науки проблема появления математики, вообще говоря, не имеет решения. Философская концепция интуиционизма состоит в признании неточности самой постановки вопроса о том, когда появилась математика либо теорема Пифагора, ибо математика как объективное проявление абстрактных закономерностей, очевидно, существовала и до Пифагора, и до возникновения вида homo sapiens.

Поэтому и вопрос о том, когда математика появилась как наука, изобретенная самим человеком, является важной, но все-таки спорной псевдопроблемой, поскольку древневавилонская математика как изобретение человека не была полностью тождественна египетской, египетская — греческой, греческая — арабской, арабская — индийской, а индийская — китайской. В такого рода историческом релятивизме новоевропейская математика отнюдь не тождественна современной, а современная математика не тождественна той, которая будет существовать в IV тысячелетии н.э., так как языки и символы математики, которые создаются и обрабатываются человеком на песке, на камне, на бумаге, на электронно-вычислительной технике всегда могут оказаться не тождественными подлинно непротиворечивой абстрактной теории.

Европейский ученый, приступающий к исследованию истории древнейшей математики всегда будет видеть лишь ее часть. Ведь из того хорошо известного историкам науки факта, что математика, естествознание, искусство, письменность и язык не отделялись в древних культурах от религии, можно заключить, что некоторое изображение или текст, понимаемые нами как «миф о сотворении мира», «ритуальная магия», «скульптура бога», имели отношение и к тем проблемам, которые мы бы назвали «математическими» или даже «чисто математическими». Например, самые древние двоичные дроби в последовательности 1/2; 1/4; 1/8; 1/16; 1/32 и т.д. назывались жрецами Верхнего и Нижнего Египта дробями бога Сета и обозначались соответствующим образом ^{[7, С.37]}. Нисколько не удивительно поэтому, что у нас вызывают снисходительную улыбку либо недоумение слова, с которых начинается древнеегипетский папирус Ахмеса, обещающий научить «совершенному и основательному исследованию всех вещей, пониманию их сути, познанию всех тайн», тогда как затем приводятся обычные арифметические примеры по подсчету количества зерна, а также правила вычисления дробей ^{[6, С.19]}.

Подобный синкретичный характер имела и математика древнего пифагорейского общества, ставшая фундаментом эллинистической математики, а также, в значительной мере, — арабской и новоевропейской математики. Ведь приписывание Пифагору теоремы о сумме квадратов катетов, равной квадрату гипотенузы, более того, приписывание ему всех поздних пифагорейских теорем были продолжением неприемлемых для позитивной науки религиозно-философских воззрений.

Имя Пифагора было для кротонских математиков священным именем, так что сами пифагорейцы предпочитали его называть «тот, оный», «божественный», а в доказательствах, восходящих к учителю, употребляли «αυτος ειπα» (греч. «сам сказал»). Для древнегреческих ученых Пифагор являлся не человеком, создавшим математическую теорию, а непосредственным воплощением космической гармонии или бога Аполлона (от греч. απολουω, «очищать») ^{[8, С.7]}, стрелой которого был убит змей Пифон на том месте, где находился священный центр земли, более известный нам как Дельфийский оракул.

Стремление взять из древнегреческой математики лишь то, что имеет практическое значение, неспособность видеть античную математику глазами самих пифагорейцев послужили предпосылками становления так называемого европейского образа мышления, в котором человек рассматривается как собственник всей материальной вселенной, как сам бог-творец высших абстрактных законов, а не как воплощенный в первочеловеке образ божественного разума. Тяжелой расплатой за пренебрежение к пифагорейской философии, за искажение и упрощение тех исторических процессов, в которых зарождались математические термины, за нежелание вникать в суть теоретических положений, приведших к первому кризису оснований математики, стало тлетворное разложение и системный кризис современной математической науки. Итак, рассмотрим общую первопричину трех обозначенных выше кризисов, а именно один из основополагающих терминов, введенных во времена античности.

ARGVMENTUM AD IGNORANTIAM

За сотни лет развития математики историки так и не сумели выработать внятного представления о том, кем было сделано открытие иррациональных чисел (от лат. irrationalis, «неразумный» — калька с греч. αλογον, «несоизмеримый», «невыразимый»). С одной стороны в древних текстах это открытие часто приписывают Пифагору (VI век до н.э.), с другой стороны — античному математику Гиппасу из Метапонта (V век до н.э.).

Вероятнее всего, это вызвано тем обстоятельством, что Пифагору было лишь известно о явлении несоизмеримости стороны и диагонали квадрата, тогда как Гиппас сумел привести этому «строгое доказательство». В самом деле, коль скоро Пифагор был знаком с передовыми идеями вавилонской математики, коль скоро пифагорейцам был известен метод «боковых и диагональных чисел» для получения приближений 3/2; 7/5; 17/12 и т.д. при вычислении гипотенузы прямоугольного треугольника с катетами, равными единице ^{[7, С.175-176]}, то основатель тайного пифагорейского общества, конечно же, не мог не знать о проблеме несоизмеримости стороны квадрата и его диагонали.

Об этом же свидетельствует и легенда о пифагорейском проклятии, насланном на Гиппаса, которого античные математики обвинили в разглашении тайны пифагорейского братства. Если бы до Гиппаса пифагорейцы не ведали понятия несоизмеримости, то его бы, разумеется, обвинили вовсе не в «разглашении», а в создании теоремы, противоречащей учению Пифагора. Вот одна из реконструкций доказательства данной теоремы, которое в историческом очерке Н. Бурбаки определяется, ни больше — ни меньше, как «наилучший классический пример рассуждения от противного в математике» ^{[9, С.300]}.

«Допустим, что диагональ квадрата AC и его сторона AB соизмеримы, то есть их отношение равно отношению двух целых чисел: AC /AB = m / n. (1)

Предполагается, что числа m и n не являются оба четными, иначе дробь можно было бы сократить на два. Из (1) следует, что AC^2 / AB^2 = m^2 / n^2. Но по теореме Пифагора AC^2 = 2AВ^2; следовательно, m^2 = 2n^2. (2)

Значит, m^2 — четно. Из учения о четных и нечетных числах следует, что в этом случае и m — четно (так как произведение двух нечетных чисел нечетно). Но тогда n — нечетно. Поскольку m — четно, то m = 2t. Подставляя в (2), получим 4t^2 = 2n^2, или n^2 = 2t^2, то есть n^2 — четно, следовательно, и n должно быть четным, что приводит к противоречию» ^{[10, С.73]}.

Эти десять строчек доказательства Гиппаса о несоизмеримости стороны и диагонали столь же неубедительны для интуициониста, как десять строчек доказательства Г. Кантора о «несчетности» множества всех действительных чисел, на что указал доктор физ.-мат. наук А.А. Зенкин ^{[11, С.165-168]}. Если у формалиста, порой неразличающего за символами их содержания, к такому «наилучшему классическому доказательству» никаких вопросов не возникает, то у историка науки может возникнуть вопрос — откуда взялась убежденность Гиппаса в том, что сторона квадрата AB и его диагональ AC — оба этих отрезка — выражаются «четными числами»? Хотя, как известно, ни сторона n, равная единице — нечетному числу(!), ни диагональ m, равная √2 =1,414..., никак не могут быть «четными числами». С нашей точки зрения гораздо логичнее было бы искать отношение m /n для √2 и доказывать, что такого отношения существовать не может, вовсе не с помощью метода четных и нечетных чисел, а с помощью правил перевода десятичных дробей в обыкновенные. Ведь число √2 =1,414... — это десятичная дробь, которая по определению не может быть ни четным, ни нечетным числом.

Оказывается, другого «строгого доказательства» несоизмеримости математики-пифагорейцы предложить просто не могли, так как они не имели представления о непрерывных десятичных дробях. Более того, даже отношения целых чисел m /n, которые мы иначе называем обыкновенными дробями, они не признавали дробными значениями, потому что в античной арифметике, в отличие от современной, действовала аксиома неделимости единицы. Единица являлась для математиков-пифагорейцев «божественной монадой», деление которой было формально запрещено. В то же время пифагорейцам была известна десятичная «космическая монада» в виде суммы чисел 1+2+3+4=10, что неявно допускало ее делимость.

Б.Л. ван дер Варден пишет об этом так: «До Архимеда дроби вообще не входили в официальную греческую науку. Но это объясняется не тем, что их не знали, но скорее тем, что их не хотели знать (...) Впрочем, следы древнего исчисления дробей обнаружить можно. В VII книге «Начал» Евклида (а эта книга, как мы увидим позже возникла до 400 года до н.э.) имеются следующие определения:

Определение 3: Число является частью другого числа, меньшее — большего, если оно измеряет большее.

Определение 4: И частями, если оно большего не измеряет.(...)

Определение 20: Числа являются пропорциональными, если первое от второго и третье от четвертого будут одинаковыми кратными, одинаковой частью или частями (...)

Терминология целочисленных отношений в пифагорейской теории гармонии также напоминает о том, что целочисленные отношения были первоначально дробями (…) Древнейший текст, где встречаются дроби, представляет «Илиада» Гомера (К 253): "Ночи две части прошли и третья осталась частица". Отсюда ясно, что дроби были известны грекам с древнейших времен и что они по крайней мере в V веке до н.э. вполне владели действиями с дробями» ^{[7, С.68-69]}.

Тогда возникают следующие вопросы: для чего пифагорейцам потребовалось вводить аксиому неделимости единицы, почему они исключали единицу из чисел, т.к. «единица не является множеством» ^{[7, С.151]}, и почему современные математики-формалисты не смущаются этими «тонкостями», полагая, что смысл терминов, возникших в пифагорейской арифметике, полностью сохраняется в арифметике непрерывных десятичных дробей, построенной на диаметрально противоположной аксиоме — аксиоме о возможности бесконечного деления единицы, то есть на возможности рассмотрения единицы в качестве множества, обладающего свойством к бесконечному уменьшению?

Все говорит о том, что пифагорейцам было известно о существовании сразу двух типов арифметики: аполлонийской («очищенной» от бесконечных процессов деления единицы) и дионисийской (тайная часть учения Пифагора, позволявшая находить «боковые и диагональные числа» при рассмотрении несоизмеримых отрезков, приводившая, однако, к бесконечному хаосу чисел). Изобретение или искусственное введение аксиомы неделимости единицы потребовалось в пифагорейской арифметике как раз для того, чтобы «оконечить» бесконечность ряда дробей, возникавших, например, при попытке соизмерения стороны и диагонали квадрата — 3/2; 7/5; 17/12 и т.д. (то есть чтобы «убить Пифона»).

Другим существенным отличием пифагорейской арифметики, вытекающим из той же аксиомы неделимости единицы, была так называемая аксиома о четности и нечетности единицы ^{[7, С.151]} (отсюда и «муже-женственные андрогинны» в учении Платона). Так как деление единицы на два давало «запрещенную» дробь 1/2, а прибавлением единицы создавались все четные и нечетные числа, то в арифметике целых чисел «андрогинный» постулат становился необходимым. Об уровне догматизма в античной математике можно судить по высказыванию Платона в трактате «Государство»: «Если ты захочешь делить единицу, то ученые математики высмеют тебя и не позволят это сделать; если же ты размениваешь единицу на мелкие деньги, они полагают ее обращенной во множество и остерегаются рассматривать единицу не как единое, но состоящее из многих частей» ^{[7, С.161]}.

В рамках такого весьма своеобразного набора аксиом пифагорейской арифметики, содержащего аксиомы неделимости и четно-нечетности единицы, доказательство Гиппаса, действительно, можно было бы признать непротиворечивым. Однако вряд ли это позволяет назвать его доказательство «наилучшим классическим примером рассуждения от противного в математике», если только в этой математике применяются бесконечные десятичные дроби.

CONCORDIA DISCORS

Ссылаясь на непререкаемый авторитет имени Пифагора, математики-пифагорейцы Феодор, Теэтет и Архит создали в IV веке до н.э. теорию несоизмеримости нецелых квадратных и даже кубических корней. Любая критика их трудов жестко подавлялась. Платон за отрицание атомистами теории несоизмеримых отрезков призывал сжигать труды Демокрита ^{[12, С.22]}, несмотря на то, что Демокрит был одним из создателей теории правильных многогранников или Платоновых тел. Судя по всему, основоположник теории пропорций Евдокс Книдский был изгнан из Афин по той же причине — за высказывание сомнений в справедливости теории несоизмеримых отрезков.

Из учения Евдокса о пропорциях (I; V; VI и XII книги «Элементов» Евклида) ^{[7, С.253-254]} следовало, что величины будут находиться в некотором отношении между собой или в пропорции, «если они, взятые кратно, могут превзойти друг друга» ^{[13, С.142]}. Поэтому в геометрии никакой принципиальной разницы между соизмеримыми и несоизмеримыми отрезками не возникало — и те, и другие отрезки оказывались в этой теории пропорциональными (от лат. proportio — «соизмеримый»). Евклидовы «Элементы» (конец IV века до н.э.), которые рассматриваются формалистами как вершина математической мысли эпохи Платона и Аристотеля, были и впрямь вершиной, но то была вершина огромного айсберга, потопившего немало теорий, включая саму античную математику. Евклид создавал свои «Элементы» в обстановке, которая отнюдь не имела ничего общего с идилистической картиной дружбы и согласия античных философов по принципиальным для развития науки вопросам.

В математике яблоком раздора была как раз теория несоизмеримых отрезков. Она являлась предметом жарких научных дискуссий между Платоном и Аристотелем. Если Платон безоговорочно принимал доказательство несоизмеримости Гиппаса и теорию несоизмеримых отрезков, то Аристотель высказывал сомнение в правильности хода умозаключений в доказательстве Гиппаса и его учеников, по сути, оказывая поддержку перспективной теории Евдокса Книдского.

В «Первой аналитике» Аристотель указывал на логическую недостаточность доказательств несоизмеримостей в теории Феодора, Теэтета и Архита, даже с учетом хорошо известных ему постулатов пифагорейской арифметики: «И таким же вот образом бывает всегда, что при делении общее берется в качестве среднего [термина], а то, что требуется доказать, и [видовые] различия берутся в качестве крайних [терминов]. В конце концов [производящие такое деление] ничего определенного не говорят (...) Очевидно, однако, что при помощи этого метода нельзя что-либо опровергнуть, как невозможно в отношении чего-либо случайного или свойственного [тому или иному предмету] вывести заключение и относительно [его] рода в тех случаях, когда неизвестно, обстоит ли дело так или иначе, как, например, соизмерим или нет диаметр [и сторона]. Если принять, что всякая длина соизмерима или несоизмерима, а диаметр и есть длина, то можно заключить [лишь то], что диаметр соизмерим или несоизмерим. Если принять, что он несоизмерим, то [этим] принимается то, что требовалось вывести в качестве заключения. [Так], следовательно, нельзя доказывать (...) Пусть соизмеримое или несоизмеримое обозначает А [то, что следует вывести], длина — Б, диаметр — В. Очевидно, таким образом, что [указанный] способ деления применим не во всяком исследовании и бесполезен в тех случаях, где он, казалось бы, больше всего подходит» ^{[14, С.90]}.

Что касается доказательства Гиппаса, то здесь схема Аристотеля тоже приводит к логической недостаточности. В пифагорейском учении о четных и нечетных числах единица (или число n в теореме Гиппаса) являлась и четным, и нечетным числом. В ходе доказательства Гиппас пришел к выводу о том, что число n — четное, но на основании этого нельзя получить опровержения тезиса о соизмеримости, так как из аксиом пифагорейской арифметики изначально известно, что число n может быть и четным, и нечетным.

В «Метафизике» Аристотель объясняет, почему он придерживается пифагорейской аксиомы о неделимости единицы и учения о четных и нечетных — оказывается, из опасения, что иначе произойдет увеличение арифметических число-сущностей: «Далее, должно было бы быть промежуточное и в таких родах, в которых отрицание влечет за собой противоположное, например, в области чисел — число, которое не было бы ни четным, ни нечетным. Но это невозможно, что ясно из определения [целых чисел]. Далее, если бы было такое промежуточное, то пришлось бы идти в бесконечность, и число вещей увеличилось бы не только в полтора раза, но и больше [множество ни четных, ни нечетных, то есть дробных чисел]. В самом деле, тогда это промежуточное можно было бы в свою очередь отрицать, противопоставляя его [прежнему] утверждению и отрицанию [взятым вместе], и это было бы нечто [новое], потому что сущность его — некоторая другая [в самом деле, после введения дробей были открыты трансцендентальные числа и многие другие классы чисел]» ^{[15, С.142]}.

Далее он предостерегает, что, опираясь на явление «несоизмеримости», можно легко вывести ошибочное умозаключение об отсутствии истины ^{[15, С.143]}. И соглашается с тем, что доказательство Гиппаса можно признать, но лишь при том принципиально важном условии, «если доказано, что для противоположностей [соизмеримые и несоизмеримые величины] существует одна и та же способность [принимать только четные или нечетные значения], тогда [окажется], что и знание о них будет одно и то же; здесь уже соглашаются и без предварительной оговорки, ибо ложность [будет] очевидной, например, если допустить, что диагональ соизмерима, то нечетное окажется равно четному» ^{[15, С.195]}.

Почему же никто из тех, кто восторженно отзывается о доказательстве Гиппаса, не уточняет, что уже Аристотелю было известно о том, что при употреблении дробей (ни четных, ни нечетных чисел) доказательство Гиппаса теряет всякую доказательную силу? Да просто потому, что в современной математике господствует так называемая теоретико-множественная парадигма, адепты которой не допускают и мысли о том, что в античной математике могло возникнуть некорректное доказательство. Но из приведенных выше примеров видно, что в самой античной математике сохранялась устойчивая традиция критически относиться к доказательствам теории несоизмеримых отрезков, несмотря на то, что значительная часть подвергших Гиппаса остракизму пифагорейцев, поплатилась жизнью во время кротонского заговора. В этой связи необходимо заметить, что из собранных Ямвлихом сведений о причинах той жестокой расправы, в результате которой десятки учеников Пифагора и сотни пифагорейцев-акусматиков были сожжены и убиты, а имущество братства было разделено между организаторами мятежа, следует нелицеприятный для истории науки факт, что в числе подстрекателей к расправе над пифагорейцами находился все тот же изгнанный из братства математик Гиппас ^{[8, С.150]}.

Накал страстей, бурливших вокруг доказательств теории несоизмеримых отрезков, в верности которых сомневались представители сразу нескольких философских школ, а также глубочайшие кризисные явления, с которыми столкнулись древнегреческие мыслители, закладывая основы стандартной математики, — все это совершенно не сочетается с тем, как склонны себе представлять античную арифметику математики-формалисты.

Выразителем этих взглядов можно считать Г. Кантора, ответившего на возражения Г. фон Гельмгольца и Л. Кронекера по поводу теоретико-множественного подхода буквально следующее: «Впрочем, у обоих ученых явно выступает наружу мотив враждебного отношения к актуально-бесконечному, и поскольку, как известно, нельзя обосновать с научной строгостью даже "конечных" иррациональных чисел без решительного привлечения к делу актуально-бесконечных множеств [здесь двойная ссылка Г.Кантора на свои статьи], то усилия обоих — в особенности Кронекера — направлены с неуклонной последовательностью на то, чтобы сделать с помощью искусственно придуманных, кажущихся им подходящими вспомогательных теорий совершенно "ненужными" и лишними [ссылка на Кронекера и Молька] всеми принятые со времен Пифагора и Платона иррациональные числа, вместо того, чтобы исследовать и объяснить их согласно их природе» ^{[16, С.98-99]}.

Так вот, «во времена Пифагора и Платона» иррациональные числа никак не могли «быть всеми принятыми», хотя бы потому, что они выражаются бесконечными десятичными дробями, которыми тогда не умели пользоваться, хотя бы потому, что в самой Пифагоровой арифметике имелась аксиома неделимости единицы, за соблюдением которой ревностно следил Платон. Приведенное выше утверждение Г.Кантора, который обо всем этом знал, есть грубое искажение истории математики, вызванное скорее одержимостью «актуально-бесконечным», нежели стремлением разобраться в природе явления «несоизмеримости».

В эпоху Платона античная наука пребывала в глубочайшем кризисе, но верно и то, что кризис этот был катализатором исследований, направленных на более строгое, формализованное описание математических понятий. Однако стремление к строгости выражалось двояко. Платон, находившийся под сильным влиянием пифагорейцев (как видно, последователей Гиппаса), часто выдавал за такую строгость синкретичный догматизм учения Пифагора, тогда как Аристотель прекрасно знал об опасности принять за истину ошибочное умозаключение, выстроенное на основании тех или иных догматов.

В частности, на это указывает отношение Аристотеля к математическим аксиомам. Под аксиомой он понимал положение, лежащее в основе доказательства, которое само не требует доказательств, а принимается в качестве общепризнанного ^{[13, С.245]}. В таком понимании нет требования «внутренней непротиворечивости» аксиом или отождествления набора аксиом с абсолютной математической истиной. Наборы аксиом рассматриваются Аристотелем в духе конвенционализма А. Пуанкаре, когда предполагается, что на смену одного определения, принятого за аксиому, могут придти другие, более точные.

Историк математики и переводчик Евклидовых «Элементов» Д.Д. Мордухай-Болтовский обнаруживает в этом представлении сходство с философией стоиков, полагавших, что любое изреченное слово нельзя полностью отождествлять с подлинно непротиворечивой мыслью или внутренним логосом: «Не так далеко отстоят от Аристотеля и стоики, допускающие в качестве аксиом как верные, так и неверные положения, но с признаками общности и фундаментальности, из которых выводятся следствия, быть может даже уничтожающие эти положения» ^{[13, С.245]}.

Для представителей школы формализма такое понимание неприемлемо, ведь они хотят как раз получить такой набор символов, который никто ничем не сумел бы опровергнуть. Однако перед Аристотелем стояла другая задача. Он понимал, что для развития математической науки необходимо было примирить математические традиции пифагорейцев, стремившихся (как «правильно, но неверно» понял Г. Кантор), «оконечить» бесконечность, с теорией Евдокса, в определениях которой бесконечность мыслилась как свойство величин к ничем неограниченному становлению, что в полной мере отвечало взглядам самого Аристотеля, утверждавшего, что бесконечное не может существовать как актуальное бытие ^{[17, С.112]}.

Только благодаря тому, что Аристотель не выдвигал требований внутренней непротиворечивости для аксиом, ему удалось решить эту задачу введением в основания математики фундаментальной аксиомы о разделении геометрии и арифметики: «Для числа имеется предел в направлении к наименьшему, а в направлении к большему оно всегда превосходит любое множество, для величин же наоборот: в направлении к меньшему оно превосходит все своей малостью, а в направлении к большему бесконечной величины не бывает. Причина та, что единица неделима» ^{[17, С.120]}.

Именно благодаря этой формулировке о разделении арифметического числа и геометрической величины стало возможно появление «Элементов» Евклида — трактата, где собраны воедино две враждовавшие между собой античные концепции. Не стоит, однако, полагать, что в современной математике дело обстоит иначе. Оттого, что математики вычеркнули «на бумаге» аксиому неделимости единицы вместе с аксиомой о разделении числа и величины, эти аксиомы никуда не исчезли из доказательств, которые были признаныкорректными«во времена Пифагора и Платона».

Напряженный труд Г. Кантора состоял как раз в том, чтобы перенести пифагорейские представления о числе, «имеющем предел в направлении к меньшему», на геометрические непрерывные величины. Он решил отказаться от аксиомы о разделении числа и величины, но пошел к этому путем пифагорейцев, предположив, будто у величин, может быть абсолютный арифметический предел в направлении к меньшему, только не единица, а кардинальное число (алеф). Вот этот гипотезис и был предложен Г.Кантором как аксиома о двух стягивающихся в общую точку отрезках. Однако теория множеств не позволила математикам адекватно описать геометрическую непрерывность в символах теории бесконечных множеств (доказательство гипотезы континуума или первая проблема Д. Гильберта).

Поэтому один из создателей системы аксиом теории множеств А. Френкель был полностью согласен с тем, что введенная Аристотелем аксиома разделения числа и величины продолжает выполняться, несмотря на все усилия, приложенные для ее устранения: «Преодоление пропасти между областью дискретного и областью непрерывного, или между арифметикой и геометрией, есть одна из главных, — пожалуй, даже самая главная проблема оснований математики (…) Характер рассуждений теперь, конечно, изменился, но трудности, как и прежде, возникли в связи с пропастью между дискретным и непрерывным — этим неизменным камнем преткновения, играющим чрезвычайно важную роль в математике, философии и даже физике» ^{[18, С.12]}.

Таким образом, в основаниях математики в период античности сложилась следующая Аристотеле-Евклидова система аксиом (АЕ):

1. Аристотелева аксиома разделения числа и величины.

2. Пифагорейская система аксиом арифметики, в том числе:

a) аксиома неделимости единицы;

b) аксиома о четности и нечетности единицы.

3. Система арифметических аксиом, выводимых из «Элементов» Евклида ^{[13, С.247]}.

4. Аксиома Евдокса-Архимеда: для любых двух отрезков А и В можно указать такое натуральное число n, что n∙B >A.

5. Евклидова система аксиом геометрии.

LOGICA VETVS ET NOVA

Несмотря на выдающиеся математические открытия поздней античности в трудах Архимеда и Аполлония, древнегреческая математика не выдержала испытания временем. Для того, чтобы обойти логические антиномии при обращении с «несоизмеримостями», античные ученые выработали особый язык геометрической алгебры. Но математические трактаты, написанные этим языком, были «необычайно трудными и большей частью не читались» ^{[6, С.358]}.

Достигнув небывалых высот, античная цивилизация пришла в упадок в круговороте нескончаемых войн. По крайней мере трижды была сожжена Александрийская библиотека (в период римских завоеваний, становления иудео-христианкой цивилизации и образования арабского халифата). Обломки античной науки были собраны в более прагматичной арабской математике, где пространный язык «греческой учености» был переведен Аль-Харезми на более емкий и доступный язык алгебры.

Новоевропейская наука, которая стала формироваться после крестовых походов, не являлась непосредственным продолжением античной математики. Средневековая схоластика взяла из античной науки лишь то, что было нужно для ведения феодального хозяйства и утверждения в умах неизменной картины мира. Сама обстановка средневековья с неограниченным могуществом церковной власти была далека от скептического настроения философов в эпоху античности.

Тем не менее, вместе с переводами арабских математических трактатов в Европе XII века утвердилась арабо-индийская десятичная система счисления. Именно влияние восточной математики привело к постепенному введению в европейскую арифметику десятичных дробей (упоминание о них содержится в «Книге об индийской арифметике» Абу-аль-Хасана Ахмада, X век). Если средневековые схоласты еще штудировали Аристотеля, повторяя положение о неделимости единицы, то после Джордано Бруно, Николая Коперника, Галилео Галилея, Иоганна Кеплера, Франсуа Виета, Пьера Ферма, Рене Декарта и многих других великих ученых XV-XVII веков никто уже не смел придерживаться столь странных арифметических анахронизмов.

Метод координат Рене Декарта и разработанная им теория измерения интервалов позволяли говорить о единой природе арифметического числа и геометрической величины. Тем самым картезианская система противопоставила себя античной теории несоизмеримости. Именно благодаря Декарту квадратичные и прочие иррациональности стали рассматриваться в качестве действительных арифметических корней. А ведь еще в 1544 году Михаэль Штифель в своей «Arithmetica integra» утверждал, что «irrationalis numerus non est verus numerus» (с лат. «иррациональные числа — не истинные числа»), исключая по давней традиции все иррациональные числа из множества действительных, ибо ни одно из них нельзя было вычислить с такой точностью, которая бы позволила говорить о реальном существовании числа, к которому выполняется приближение ^{[1, С.135]}.

Выражая полное согласие с Рене Декартом по поводу «равенства прав» между числами рациональными и иррациональными, современные математики едва ли вспоминают, что причиной установления этого равенства служила убежденность Декарта в том, что дальнейшее изучение иррациональных чисел позволит открыть их «простую природу». Пожалуй, из всего поколения математиков той великой эпохи только основатель анализа Рене Декарт интуитивно догадывался о наличии в математике фундаментальных противоречий. В своих «Правилах для руководства ума» он высказывал подозрение, что античные авторы «из пагубной хитрости утаили» от потомков истинную сущность математики, заменив ее другими,«остроумно выведенными истинами» ^{[19, С.67]}.

Все попытки выявления «пагубной хитрости» античной математики закончилась для Декарта без ожидаемого результата. Однако Рене Декарт впервые сформулировал эпистемологическую проблему о том, возможно ли построение математики без применения Аристотелевой аксиомы о разделении арифметики и геометрии? Открытие дифференциального исчисления сэром Исааком Ньютоном и Готфридом Вильгельмом Лейбницем, а также развитие математического анализа в XVIII веке, по сути, было попыткой дать положительный ответ на этот картезианский вопрос. Однако в новоевропейской математике не обращали внимания на аксиомы арифметики и геометрии — они полагались как некая тривиальная данность, неизменный набор самоочевидных истин. Поэтому никто не пытался дать исчерпывающее объяснение, отчего некоторые пифагорейские теоремы на проверку оказывались некорректными (как показал Пьер Ферма в своей Великой теореме), поэтому полной неожиданностью для математиков XVIII века оказалось обнаружение парадоксов бесконечно малых величин.

Как известно, дьявол кроется в мелочах, а математический дьявол скрывался на этот раз в бесконечно малых величинах. При вычислении производных функций требовалось определение мгновенной скорости, то есть пройденное физическими телами «нулевое» расстояние нужно было делить на «нулевое» же время, что давало не имеющее математического смысла выражение 0/0 (на ноль делить нельзя). В решении этого затруднения существовали два подхода: сэр Исаак Ньютон категорически возражал против употребления «неделимых в пределе», выступая за представление бесконечно малых в качестве бесконечно убывающих величин, а Лейбниц настаивал на том, что, бесконечно убывая, величины могут достигать некоторых особых «бесконечно малых значений». Он их определял как отношение dy/dx, удовлетворяющее строгому тождеству, ибо ошибка в данном случае будет «меньше любой конечной величины» ^{[1, С.162]}.

В стандартной математике получили развитие абстрактно-логические взгляды Лейбница, применявшего следующий принцип непрерывности: «Если переменная на всех промежуточных этапах обладает некоторым свойством, то и ее предел будет обладать тем же свойством», — хотя этот принцип «не был (и ныне не является) математической аксиомой» ^{[1, С.163-164]}, но он оказался очень удобным для обоснования математического анализа. Математикам не нужно было задумываться над каждым решением, сравнивая конкретные бесконечно малые величины.

Вот что сообщает по этому поводу советский историк и философ математики С.А. Яновская: «Всякий обучающийся теперь дифференциальному исчислению уже на первых шагах обучения сталкивается с теоремой Ролля. Но лишь немногим известно, что Ролль был горячим противником того самого дифференциального исчисления, успеху которого он содействовал не только своей теоремой, но и своими выступлениями против анализа бесконечно малых» ^{[20, С.76]}. Мишель Ролль критиковал методы, ставшие стандартными методами анализа, поскольку считал, что «мы впадаем в противоречие, приписывая протяженность бесконечно малым dx и dy. И это противоречие становится тем большим, чем больше увеличиваем мы эту протяженность. Ибо, если мы берем, например, 4 вместо бесконечно малого dy, тогда равенство dy=0 изменится в 4=0, и это противоречие станет бесконечно малым, если вместо 4 мы подставим бесконечно малую величину» ^{[20, С.96]}.

В наши дни Ролля обвинили бы в лукавстве, ведь он вместо бесконечно малой величины брал конечное целое число 4, приравнивая его к 0 — к «абсолютному ничто». Однако ему было важно показать, что некое противоречие все же возникает. В самом деле, применение десятичных дробей позволяет нам записать равенство 3,(9)=4, то есть 3,(9)+0,(0)1=4,(0), где 0,(0)1 — бесконечно малая единица. Если оба эти равенства тождественны, если мы можем «обнулить» или «уничтожить» бесконечно малую единицу, то все бесконечно малые, из которых состоит 3,(9)=4, тоже можно «обнулить», но тогда мы получим как раз 4=0, причем это следует из того же принципа непрерывности Лейбница.

Мишель Ролль хотел получать вместо бесконечно малых приближений некие точные значения, как в арифметике целых чисел, что, конечно же, было невыполнимо, но его возражение вскрывает «филогенез» стандартной математики, который был далек от совершенства. Если Лейбниц осознавал существование погрешности при «уничтожении» бесконечно малых, то Леонард Эйлер в своем «Дифференциальном исчислении» предлагал математикам прекратить споры и «забыть» о приращениях бесконечно малых величин, объясняя это тем, что «никаких глубоких таинств, как полагают обычно, что и делает исчисление бесконечно малых для многих чрезвычайно подозрительным, здесь не скрывается» ^{[20, С.101]}.

Вероятно, многих ошибок можно было бы избежать, если бы хоть кто-то из основателей анализа догадался связать стремительное введение в математику бесконечных десятичных дробей с появлением нового набора арифметических аксиом, который не применялся в античной математике. Ведь вместо аксиомы о неделимости единицы появилась аксиома о возможности бесконечного деления единицы. Вместо множества действительных чисел, состоящих только из целых чисел (четных или нечетных) появилось множество действительных чисел, состоящее из целых и дробных чисел (четных, нечетных, а также — ни четных, ни нечетных). Стало быть, и применимость Аристотелевского принципа «tertium non datur» (с лат. «третьего не дано») в доказательстве Гиппаса при помощи четных и нечетных чисел следовало подвергнуть тщательнейшей проверке.

CONTRADICTIO IN ADJECTO

Однако осознание необходимости систематического изучения аксиом возникло у математиков лишь в XIX веке, прежде всего, благодаря исследованиям Г.Ф. Гаусса, Н. Лобачевского и Я. Бояи, показавших, насколько разительно могут отличаться свойства одних и тех же, казалось бы, объектов при их рассмотрении в рамках различных наборов геометрических аксиом. Парадоксы, возникающие между аксиомами арифметики и геометрии по достоинству оценил Юлиус Вильгельм Рихард Дедекинд. Спустя сотни и даже тысячи лет после написания Евклидом сводного трактата по основам античной математики, Р. Дедекинд заметил нестыковку аксиомы измерения Евдокса-Архимеда (V книга «Элементов») с несоизмеримыми отрезками длины, которые возникают в последующих книгах трактата.

В математическом сочинении «Непрерывность и иррациональные числа» Р. Дедекинд пишет: «Фактом величайшей важности является то обстоятельство, что на прямой L есть бесконечно много точек, которые не соответствуют никакому рациональному числу. Действительно, если точка "p" соответствует рациональному числу "a", то, как известно, длина "0р" соизмерима с употребленной при построении единицей длины, то есть существует третья длина, так называемая общая мера, относительно которой обе длины представляются целыми кратными. Но уже древние греки знали и доказали, что существуют длины, несоизмеримые с данной единицей длины, — например, диагональ квадрата, сторона которого есть единица длины. Если нанести такую [несоизмеримую] длину от точки "0" на прямую, то получим конечную точку, которой не соответствует никакое рациональное число» ^{[21, С.15]}.

Несмотря на то, что Р. Дедекинд нисколько не сомневался в доказательстве Гиппаса, он вновь обратил внимание математиков на существующую с незапамятных времен проблему разделения арифметического числа и геометрической величины: «Принятое до сих пор введение иррациональных чисел связывается именно с понятием о протяженных величинах — которое само нигде не определено — и определяет число как результат измерения такой величины другою такого же рода. Вместо этого я требую, чтобы арифметика развивалась сама из себя (…) чтобы иррациональные числа были вполне определены через посредство рациональных. Но как это сделать —вот в чем вопрос» ^{[21, С.16]}.

Ответ был найден Р. Дедекиндом в том, чтобы вместо соизмеримых и несоизмеримых отрезков взять два класса P и Q, таких что каждая точка первого класса лежит влево от каждой точки второго, при этом существует одна и только одна точка α, которая производит сечение прямой на два класса ^{[21, С.24]}. Однако такая непрерывность числовой прямой достигалась за счет того, что точка сечения двух классов относилась к первому или ко второму классу совершенно произвольно, откуда следовала возможность отнести все точки прямой к какому-то одному классу, либо к классу рациональных, либо к классу иррациональных чисел. Поэтому Дедекинд соглашался с тем, что он в своем предложении ничуть не приоткрывает тайну непрерывности, ибо «решительно не в состоянии привести какое бы то ни было доказательство справедливости этого принципа, и никто не в состоянии. Принятие этого свойства прямой линии есть не что иное как аксиома, посредством которой мы только и признаем за прямой ее непрерывность» ^{[21, С.18]}.

Совершенно иного представления о непрерывности придерживался Г. Кантор. Если для Р. Дедекинда непрерывность состояла в наделении одним и тем же свойством классов соизмеримых и несоизмеримых величин, то Г. Кантор считал все целые числа «прототипом разрывности», хотя ему, само собой разумеется, было известно, что любое целое число можно представить непрерывной десятичной дробью с периодом (9). Несмотря ни на что, непрерывность, по мнению Г. Кантора, следовала только из свойства несчетности множества действительных чисел, то есть была связана лишь с «несоизмеримыми величинами». Различные взгляды на природу континуума послужили поводом для научной дискуссии между Р. Дедекиндом и Г. Кантором. И здесь мы вновь сталкиваемся с фальсификацией реальной истории математики.

Представители господствующей теоретико-множественной парадигмы сумели убедить всех математиков, что между Р. Дедекиндом и Г. Кантором не существовало никаких принципиальных расхождений в понимании непрерывности. В «Википедии», а также во многих других статьях и математических пособиях, аксиомы непрерывности Р. Дедекинда и Г. Кантора даже принято именовать неким общим термином «аксиома непрерывности Дедекинда-Кантора». Но, на самом деле, Р. Дедекинд признавал теорию Г. Кантора с той опять-таки принципиально важной оговоркой, что в будущем удастся разрешить проблему непрерывности или континуум-гипотезу Г. Кантора. Раз гипотеза континуума Г. Кантора (первая проблема Д. Гильберта) до сих пор не доказана и, как следует из результатов американского математика П. Коэна, вряд ли когда-нибудь будет доказана, то и отождествлять две эти аксиомы нельзя.

Об этом различии двух аксиом говорит сам Г. Кантор в своей переписке с Р. Дедекиндом: «Вы говорите, что аксиома, указанная мною, по существу эквивалентна аксиоме, изложенной Вами в §3 [сочинения "Непрерывность и иррациональные числа"] как выражение сущности непрерывности. Однако под этим Вы понимаете то же самое свойство, которое на стр.25 дается под номером IV; но это свойство принадлежит и системе всех целых чисел, которые, тем не менее, можно рассматривать как прототип разрывности (…) [поэтому] не следует приписывать свойству IV используемого Вами наименования "сущность непрерывности"» ^{[22, С.335]}.

В ответ Р. Дедекинд указал Г. Кантору на его предвзятое отношение к целым числам: «После Вашего последнего письма мне кажется, что нам угрожает риск спора скорее о словах, чем о вещах. Всякий внимательный читатель моей работы определенно поймет мое мнение о непрерывности следующим образом: области, элементы которых сопоставляются и пополняются в форме, выраженными свойствами I и II (…) еще не обязательно являются непрерывными областями; такие области приобретают свойство непрерывности присоединением свойства IV (…) и только этого свойства» ^{[22, С.335-336]}. Четвертым свойством, вокруг которого шел спор, было как раз распространение Р. Дедекиндом представления о непрерывности как на класс рациональных, так на класс иррациональных чисел, что никак не согласовалось с теорией Г. Кантора, где последовательность целых чисел {1, 2, 3, 4... и т.д.} была обозначена «счетной» или понетциально-бесконечной, а последовательность √2 ={1, 4, 1, 4, 2... и т.д.} — «несчетной» или актуально-бесконечной, причем по доказательству Г. Кантора, которое А.А. Зенкин подверг обоснованной критике, выходило, что множество всех действительных чисел тоже являлось «несчетным» или не-нумеруемым.

Г. Кантор не допускал и мысли о том, что в его суждениях может содержаться ошибка. Более того, он твердо верил в то, что его теория создавалась при непосредственном содействии сверхразумных сущностей: «Мои дорогие друзья, любящие называть себя математиками, могут думать о моих идеях все, что угодно, они могут писать о том, что им кажется правильным, в Лондон, Париж, хоть на Камчатку, но я твердо знаю, что идеи, над которыми я тружусь со своими слабыми силами, будут занимать мыслящие умы целых поколений (...) Я далек от того, чтобы приписывать мои открытия личным достоинствам, потому что я есть лишь инструмент некой высшей силы, которая будет работать и после меня, тем же самым образом, как она проявила себя тысячи лет назад в Евклиде и Архимеде» ^{[23, цитируется по обложке]}. Весь вопрос в том, что это была за «высшая сила», которая водительствовала Г. Кантором в его исторических исследованиях? Был той силой бог или же безобразная пародия на бога?

Болезненные переживания доводили Г. Кантора до того, что он призывал полностью прекратить «бесцельные» исследования потенциально-бесконечного, апеллируя к дифференциальному исчислению, где со времен Лейбница было принято «обнулять» бесконечно малые величины ^{[22, С.71]}, и забывая сказать, что лейбницевская концепция «оконечивания» бесконечно малых подразумевала существование пренебрежимой ошибки, о которой прекрасно знали и Ньютон, и Лейбниц, и многие другие основатели анализа.

Ничем не ограниченную, свободно становящуюся потенциальную бесконечность Г. Кантор понимал как «довольно скромный и простой принцип, который рекомендуется всем как Ариаднова нить. Он должен служить тому, чтобы удержать полет математической фантазии и спекуляции в надлежащих границах, где они не рискуют попасть в бездну "трансцендентного", туда, где, как говорится в целях назидания и спасительного страха, "все возможно"» ^{[22, С.72]}. Кто знает, если бы Г. Кантор все-таки воспользовался той спасительной нитью Ариадны, то его, быть может, и не коснулось дионисийское безумие, о котором древние пифагорейцы предупреждали всякого, кто приступал к изучению математики и оказывался в лабиринтах бесконечности — там, где с древнейших времен дерзновенные мыслители надеялись обрести мудрость, а между тем постепенно теряли разум.

Практически сразу после создания теории бесконечных множеств в ней стали возникать многочисленные парадоксы. Доказать континуум-гипотезу (необходимое условие, выдвинутое Р. Дедекиндом для принятия теории Г. Кантора) ни у кого не получалось. По этой гипотезе каждое бесконечное множество подмножеств, начиная с множества всех действительных чисел, равно следующему по номеру актуально бесконечному множеству. Пытаясь найти доказательство такому «очевидному факту», Г. Кантор обнаружил лишь то, что само множество всех трансфинитных чисел ω должно было включать в качестве подмножества само себя и оказаться больше самого себя, что приводило к абсурду. По отношению к множеству всех действительных чисел это означало, что Г. Кантор предложил задавать их непрерывность трансфинитными числами, которые сами не являлись и не могли являться частями (подмножествами) некоторой непрерывной области.

Поэтому, действительно, не иначе как «криком души выступает письмо от 28 августа 1899 г. [ХLVI], в котором он [Г. Кантор] признает недоказуемость непротиворечивости существования основных объектов своей теории — вполне упорядоченных множеств и алефов, включая конечные, и предлагает принять факт их непротиворечивости за простую недоказуемую истину, за аксиому» ^{[22, С.386]}. В критический для теории множеств момент ей оказал поддержку выдающийся математик-формалист Д. Гильберт, изрекший свою знаменитую фразу: «Никто не сможет изгнать нас из трансфинитного рая, созданного Г. Кантором», — не заметив, что уже сам создатель этого «рая» изгнал из него всех математиков, предложив вместо надежных знаний зыбучие пески противоречий и пустыню ничем не обоснованных гипотез, нарушавших, помимо прочего, переместительный и распределительный законы арифметики ^{[24, С.25,75]}.

Даже сам Д. Гильберт, в конце концов, был вынужден признать, что «состояние, в котором мы находимся сейчас в отношении парадоксов [теории множеств], на длительное время невыносимо. В математике — в этом образце достоверности и истинности — образование понятий и ход умозаключений, как их всякий изучает, преподает и применяет, приводят к нелепостям. Где же тогда искать надежность и истинность, если даже само математическое мышление дает осечку?» ^{[18, С.136]}.

Если Д. Гильберт полностью поддержал теорию множеств Г. Кантора, полагая, что для нее можно будет задать непротиворечивую систему аксиом, то А. Пуанкаре придерживался на этот счет другого мнения. В философско-математическом трактате «Наука и гипотеза» он в противовес Д. Гильберту поставил следующий вопрос: «Являются ли аксиомы, явно формулируемые в пособиях, единственными основаниями геометрии?» ^{[25, С.36]}, — и указал на существование скрытых аксиом (implicit axioms), содержащихся в доказательствах, которые с формальной точки зрения являются совершенно безупречными и «очевидными».

От внимательного взгляда А. Пуанкаре не могло ускользнуть, что Р. Дедекинд, Г. Кантор и Д. Гильберт исходили из положения о непротиворечивости Евклидовой геометрии. И когда в теории Г. Кантора обнаружились парадоксы, они продолжали видеть в геометрии Евклида пример аксиоматической строгости, испытывая недоумение, почему в теории множеств, которая из нее как бы «естественным образом» вытекала, возникали многочисленные трудности. Поиск противоречий в аксиомах арифметики и геометрии привел Д. Гильберта к созданию аксиоматической теории. Ему удалось установить, что система аксиом стандартной математики не содержит внутренних противоречий, если только не содержит противоречий применяемая в ней система аксиом арифметики.

Следующим логическим шагом, как рассчитывал Д. Гильберт, должно было стать доказательство непротиворечивости системы аксиом арифметики. В пояснении к данной проблеме он писал, что «если какому-нибудь понятию присвоены признаки, которые друг другу противоречат, то я скажу, что это понятие математически не существует» ^{[26, С.26]}.

Зная о том, что в стандартной математике признается доказательство несоизмеримости Гиппаса, содержащее скрытую аксиому о неделимости единицы, и, зная о том, что применение десятичных дробей подразумевает наличие другой скрытой аксиомы о возможности бесконечного деления единицы, мы можем на основании результатов Д. Гильберта заключить, что в той математике, которую формалисты называют «образцом истинности», математически не существует основополагающее понятие — «единица».

Более того, Д. Гильберт оказался прав в том, что, если в аксиомах арифметики содержится противоречие, то в аксиомах геометрии тоже должно содержаться эквивалентное ему противоречие. И такое противоречие было обнаружено математиком-фибоначчистом А.П. Стаховым при создании алгоритмической теории измерения. Так, арифметической аксиоме о бесконечной делимости единицы соответствует геометрическая аксиома Евдокса-Архимеда, задающая потенциальную (незавершенную) бесконечность, а пифагорейской аксиоме о неделимости единицы соответствует геометрическая аксиома Г. Кантора о двух стягивающихся в общую точку отрезках, которая допускает существование актуальной (завершенной) бесконечности ^{[27, С.26]}. Таким образом, получается, что одно понятие «бесконечность» наделяется в стандартной математике диаметрально противоположными свойствами, а значит, в соответствии с определением Д. Гильберта, в ней не существует другое основополагающее понятие — «бесконечность».

Так какую же математику можно строить в течение двадцати пяти столетий, опираясь на «математически несуществующие» понятия «единица» и «бесконечность»? Интуиционист Л. Брауэр называл такую математику «патологической», а выдающийся советсткий математик А.Н.Колмогоров — «псевдоматематикой», и с этим трудно не согласиться.

FALSA IN VNO, FALSA IN OMNIBVS

В то время, когда сторонники аксиоматической теории Э. Цермело и А. Френкель разрабатывали стандартную систему аксиом теории множеств (ZF), стараясь исключить из рассмотрения парадоксальные множества, подобные множеству всех трансфинитных чисел ω, голландский математик Л. Брауэр доказал в 1909-1911 годах теорему об инвариантности числа измерений n-мерного многообразия, а также инвариантности находящихся в нем точек.

Одним из следствий теоремы Л. Брауэра был закономерный вывод о том, что аксиома о двух стягивающихся в общую точку отрезках абсурдна, — вся теория бесконечных множеств оказывалась в этом случае «патологическим казусом» ^{[18, С.148]}, поскольку в аксиоме Г. Кантора предполагалось существование непрерывного топологического перехода из 1-мерного пространства (длина вложенных отрезков) в 0-мерное (точка на числовой прямой), что невозможно, как невозможно построение идеального «perpetuum mobile» (с лат. «вечный движитель»). Без преувеличения теорема Л. Брауэра являлась для математики философским тезисом «ex nihilo nihil fit» (с лат. «из ничего ничто не появляется»). Из той же теоремы следовало и то, что «обнуление» или «уничтожение» бесконечно малых величин в дифференциальном исчислении было всего лишь условной договоренностью, равно как само употребление нулевого значения в качестве некоторого абсолютного пустого множества.

Открытие Л. Брауэра подтверждало справедливость подозрений Л. Кронекера, критиковавшего теорию иррациональных чисел и теорию бесконечных множеств. По существу, Л. Брауэр возвращал математиков к тем вопросам, которые оказались неразрешенными во время зарождения новоевропейской науки. Он, наконец, предложил то, что мог бы сформулировать еще Декарт, а именно поставить под сомнение применимость принципа «tertium non datur» в тех случаях, где третье как раз было дано. Д. Гильберт, чья вера в непротиворечивость аксиом арифметики подверглась после открытий Л. Брауэра серьезным испытаниям, обрушился на своего бывшего ученика с разгромной критикой, утверждая, что ограничение области применения закона исключенного третьего равносильно отказу от математики ^{[18, С.150]}. В конце концов Л. Брауэр был изгнан из редколлегии влиятельнейшего математического журнала «Mathematische Annalen», а его рукописи были утеряны либо, судя по уровню бурливших страстей, были просто похищены адептами теории множеств Г. Кантора.

Впрочем, ничего неожиданного в этом нет, если вспомнить, каким притеснениям и гонениям задолго до этого подвергались кротонские пифагорейцы, отвергшие Гиппаса, атомист Демокрит, Евдокс и даже Аристотель, покинувший Афинскую акадэмию из-за разногласий с Платоном. Драматическая конфронтация интуиционистов и формалистов в XX веке есть довольно точная хронологическая калька первого кризиса в основаниях математики, который разразился сразу же после появления судьбоносного доказательства несоизмеримости стороны и диагонали квадрата.

Более того, не только в математике, но и в большой науке вообще конкуренция различных теорий редко когда велась честными методами. Как результат – выживали и выживают обыкновенно только те теории, которые ведут себя наиболее агрессивно и беспощадно к своим конкурентам, уничтожая, порой, целые научные школы, имеющие вполне определенные достижения и способные эволюционировать в более совершенные теории.

Например, практически одновременно с установлением теоретико-множественной парадигмы в математике произошла смена господствующей парадигмы в физике. В массовое сознание был внедрен миф о том, что первооткрывателем теории относительности был А. Эйнштейн, хотя реальная история науки свидетельствует о том, что зачатки этой теории имелись уже в трудах Галилео Галилея, а в конце XIX века теоретическую базу для этой теории создал Г. Лоренц в статьях «Электромагнитная теория Максвелла и ее приложение к движущимся телам» и «Относительное движение Земли и эфира» (1898 г.), где был описан эффект сокращения размеров тел в направлении движения. В 1892 году А. Пуанкаре в статье «Измерение времени» доказал относительность понятия одновременности событий, ввел принцип постоянства скорости распространения света, а в 1900 году все тот же А. Пуанкаре предложил физикам знаменитую формулировку ∆m = ∆E/c^2 или E = m∙c^2.

Как справедливо заметил член-корреспондент РАН В.Ф.Журавлев по весьма странному (и вряд ли случайному) совпадению именно рецензия А. Пуанкаре на «пионерскую» работу Милевы Марич и Альберта Эйнштейна «К электродинамике движущихся тел» (1905 г.) оказалась единственным за всю историю существования журнала «Annalen der Physik» материалом, совершенно бесследно исчезнувшем из редакционного архива ^{[28, P.32]}. Если к этому добавить, что уравнения, описывающие геометрические свойства пространства-времени, названные именем А. Эйнштейна, на самом деле составил математик Д. Гильберт, то вообще окажется непонятно, на основании чего общепризнанной в истории современной науки считается версия, будто основателем теории относительности был А. Эйнштейн.

К подобным искажениям реальной истории науки, вызванных агрессивностью, а в некоторых случаях даже недобросовестностью ученых, ведущих между собой настоящую «войну на уничтожение», можно отнести и фальсификацию периодической таблицы химических элементов Д.И. Менделеева. Ведь историкам науки прекрасно известен тот факт, что сам Д.И. Менделеев перед элементами первого периода (водорода и гелия) помещал в своей таблице еще и нулевой период, куда входил гипотетический элемент «короний» и элемент X, вокруг которого слагаются все химические элементы, который есть «предельный элемент с ничтожно малым атомным весом, неспособный к химическим взаимодействиям и обладающий чрезвычайно быстрым собственным частичным (газовым) движением. Эти свойства, быть может, должно приписать атомам всепроникающего эфира» ^{[29, С.VII, 460]}.

На первый взгляд эти убеждения великого русского ученого могут показаться типичным «псевдонаучным бредом», который необходимо уничтожать в самом зародыше. Однако в 2012 году из ЦЕРН поступило сенсационное сообщение о том, что усилиями многих сотен физиков наконец-таки был обнаружен так называемый «бозон Хиггса» – частица, не вступающая в химические реакции, которую сами физики окрестили «частицей бога», из которой состоит материя. Сопоставляя описание Д.И. Менделеева со свойствами этой частицы, можно прийти к заключению, что никакой «псевдонауки» в концепции русского химика вовсе не было, зато было феноменальное теоретическое предсказание, о котором сами ученые давным-давно забыли, но которое нашло практическое подтверждение спустя столетие стремительного развития теоретической физики.

Все эти примеры показывают, насколько важно отличать реальную историю науки от той истории, которую пишут представители господствующей научной парадигмы, ведь при внимательном изучении «отброшенных теорий», в них можно найти ключ к решению проблем, которые не могут быть решены в рамках «стандартных теорий». То же самое можно сказать о математических теориях. И если мы попытаемся вернуться к теориям, критиковавшим «наилучший классический пример рассуждения от противного в математике», то обнаружим, что доказательство несоизмеримости стороны и диагонали квадрата, приведенное Гиппасом, является причиной фундаментального аксиоматического противоречия, которое невозможно разрешить в рамках «стандартной арифметики».

Для того, чтобы продемонстрировать неадекватность доказательства Гиппаса, достаточно применить его метод к целому числу 2 и «доказать», что в Аристотеле-Евклидовой системе аксиом (AE) число 2 тоже будет «иррациональным». В самом деле, пусть даны два отрезка AC=2 и АВ=1. Нам известно, что AC=2АВ. Докажем, что число 2 несоизмеримо с единицей, в точности повторяя ход размышлений из доказательства Гиппаса:

«Допустим, что AC и AB соизмеримы, то есть их отношение равно отношению двух целых чисел: AC / AB = m / n. (1)

Предполагается, что числа m и n не являются оба четными, иначе эту дробь можно было бы сократить на два. Возведем выражение (1) в квадрат: AC^2 / AB^2 = m^2 / n^2. Нам известно, что AC=2АВ; следовательно, AC^2=(2АВ)^2, то есть m^2 = (2n)^2. (2)

Так как 2n — четно, то будет четным и (2n)^2, а значит, m^2 — тоже четно. Из учения о четных и нечетных числах следует, что в этом случае и m — четно (так как произведение двух нечетных чисел нечетно). Но тогда n — нечетно (иначе дробь m / n окажется сократимой). Поскольку m — четно, то m = 2t.

Подставляя в (2), получим 4t^2 = (2n)^2, откуда n^2 = 4t^2 / 4.

Очевидно, что это выражение можно записать как n^2 = 2 ∙ 2t^2 / 4.

Поскольку в пифагорейской арифметике действует аксиома неделимости единицы, то есть в ней не существует дробных чисел, мы можем приравнять выражение 2t^2 / 4 к некоторому числу k, тогда окажется, что n^2 = 2k. Тогда можно сказать, что число 2k — четное, следовательно, число n^2 — тоже четное. Если n^2 — четное, то и число n должно быть четным, что приводит к противоречию».

Раз оба числа m и n оказались четными, то между отрезками AC=2 и АВ=1 не существует отношения, выразимого целыми числами, и нам не остается ничего другого, как перейти к утверждению, что эти отрезки — несоизмеримы! Здесь мы использовали те же самые аксиомы, которые применял в своем доказательстве Гиппас, и если математики-формалисты признают доказательство несоизмеримости стороны и диагонали квадрата «наилучшим» и «классическим», то мы вправе ожидать от них того, чтобы и доказательство несоизмеримости отрезков AC=2 и АВ=1 тоже стало общепризнанным и «классическим». Тогда бы нам не составило труда доказать несоизмеримость, вообще говоря, любых отрезков.

Из обнаружения «иррациональности» числа 2 можно сделать вывод, что губительна для математики вовсе не философия интуиционизма, а догматическая косность формализма. Математики-формалисты, убежденные в непротиворечивости теории несоизмеримых отрезков, в упор не хотят замечать, что если вместо диагонали AC в доказательстве Гиппаса поставить дробь m=1,414…, а вместо числа t поставить дробь 0,7071…, то тогда мы получим вполне адекватное арифметическое выражение n^2 = 2t^2, а именно 1^2=2(√2/2)^2. В таком случае число n=1 останется нечетным числом (то есть таким, которое при делении на два не дает целого числа), и никакого опровержения, когда оба числа m и n оказываются «четными», тогда не возникает. Как не возникает никакого опровержения, если в нашей теореме об «иррациональности» числа 2 вместо t поставить единицу, а вместо k — ни четную, ни нечетную дробь 1/2, некорректно запрещенную в AE принципом «tertium non datur» .

Разумеется, число 2 является соизмеримым с единицей, но в рамках стандартной математики, признающей «классическое» доказательство иррациональности √2, был получен интересный с точки зрения логики результат: формула А «число √2 есть число иррациональное» выводится по тем же самым правилам, по которым выводится формула B «число 2 есть число иррациональное». Раз первая формула признается истинной, то и вторая формула должна быть признана истинной. В то же время в стандартной математике число 2 считается рациональным, следовательно, вторую формулу мы должны признать неистинным суждением или –В.

В статье «О принципе tertium non datur» А.Н. Колмогоров дополнил Гильбертову систему аксиом логики суждений аксиомой отрицания, выражающей собой принцип противоречия, без которого нельзя обосновать применение самого метода reductio ad absurdum ^{[30, С.652]}.

(5) (А → В) → {( А → –В) → –А}.

«Смысл ее таков: если из А следует и истинность, и ложность некоторого суждения В, то само суждение А ложно» ^{[30, С.652]}. Далее, поскольку обе Гильбертовы аксиомы отрицания не удовлетворяют интуитивистской логике суждений, А.Н. Колмогоров выводит систему аксиом общей логики суждений, в которой, наряду с четырьмя Гильбертовыми аксиомами следования, берется аксиома отрицания (5), а также систему аксиом частной логики суждений, область применения которой ограничена и включает в себя аксиому (6) двойного отрицания:

(6) – –А → А.

Затем А.Н. Колмогоров показывает, что из этих систем аксиом общей и частной логики суждений можно доказать все формулы «традиционной» логики суждений, что подтверждает справедливость введения А.Н. Колмогоровым аксиомы (5). Математику, где принцип «tertium non datur» употребляется вне области его применимости, А.Н. Колмогоров называет «псевдоматематикой», выводы которой обладают свойством «псевдоистинности». Поскольку в теории бесконечных множеств незаконно используется принцип исключенного третьего, то вся она оказывается «псевдоистинной». Но свойство «псевдоистинности», как отмечат А.Н. Колмогоров, любопытно еще и тем, что многие выводы истинной (непротиворечивой) математики могут оказаться ничем не отличимыми от выводов стандартной («псевдоистинной») математики.

Так, арифметика целых чисел в истинной и «псевдоистинной» математике будет ничем неотличима. Во многом неотличимо и ньютоновское дифференциальное исчисление от лейбницевского. Поэтому, в частности, и теорема Ролля используется в стандартном анализе, хотя сам Ролль упорно критиковал «уничтожение» бесконечно малых. В расширенном смысле можно говорить о том, что многие выводы-открытия «псевдонауки» могут быть ничем неотличимы от выводов-открытий истинной науки. На этом же свойстве зиждется процесс смены научных парадигм, описанный в замечательном очерке Т.Куна ^[31]. Например, возможность открытия кислорода Лавуазье, который придерживался псевдонаучной теории «теплорода».

Единственное, что оставалось сделать А.Н. Колмогорову для того, чтобы доказать внутреннюю противоречивость стандартной математики, так это перевести трансфинитные суждения, где трудно получить какой-либо положительный вывод В из чистого отрицания –А, в финитные суждения ^{[30, С.662]}. Именно такой перевод мы только что осуществили в доказательстве «иррациональности» числа 2. В самом деле, если учесть, что число √2 в суждении А получается операцией извлечения квадратного корня из числа 2, суждение В о котором было получено тем же путем, что суждение А, то можно записать, что А → В, точно так же, как В → А. Такая логическая конструкция как раз соответствует аксиоме (5) или принципу противоречия А.Н. Колмогорова:

(5) (А → В) → {( А → –В) → –А}.

Если из А «число √2 есть число иррациональное» вытекает B «число 2 есть число иррациональное», а также –В «число 2 есть число рациональное», то в данном случае имеет место –А «число √2 есть число рациональное». Вывод –А получен в рамках общей интуиционистской логики суждений без применения аксиомы двойного отрицания. Это означает, что не все «псевдоистинные» выводы стандартной математики совпадают с выводами непротиворечивой математики (по Л.Брауэру). Существуют и такие, которые задают существенное отличие стандартной математики от истинной или более непротиворечивой математики, где исключено некорректное употребление принципа «tertium non datur».

AB ACTV AD POTENTIAM

Но, быть может, в рамках стандартной математики можно доказать иррациональность √2 каким-то другим способом, без некорректного употребления принципа «tertium non datur»? В самом деле, рассмотрим тривиальное конструктивное доказательство несоизмеримости √2, основанное на правилах перевода десятичных дробей в обыкновенные:

«Теорема: десятичная дробь √2=1,414… несоизмерима в целых числах p и q.

Доказательство. Рассмотрим числа p и q, такие что p^2=2q^2. Так как любое рациональное число можно записать в виде бесконечной десятичной дроби, а при переводе из десятичных дробей в обыкновенные в знаменателе мы получаем конечную последовательность из девяток, то запись целых чисел p^2/q^2=2 будет иметь такой вид p^2/999_^2=2, откуда p^2=2 · 999_^2=199_600_2. Как видим, число 199_600_2 оканчивается на 2. Получить такую последовательность в десятичной системе счисления можно лишь возвышением в квадрат некоторого целого числа, на конце которого стоит одно из целых чисел от 0 до 9, которое при возвышении в квадрат на конце образуемой последовательности дает число 2. Перебором целых чисел от 0 до 9, возведенных в квадрат, легко установить, что ни одно из них не дает на конце число 2:

0^2=0; 1^2=1; 2^2=4; 3^2=9; 4^2=16; 5^2=25; 6^2=36; 7^2=49; 8^2=64; 9^2=81.

Следовательно, искомого таким способом целого числа p — не существует».

Неужели принцип противоречия А.Н. Колмогорова, по которому мы пришли к выводу –А «число √2 есть число рациональное», дал сбой? Не будем торопиться делать скороспелое заключение. Так как число 2 — целое и не является «квадратным» целым числом (как числа 4, 9, 16, 25 и т.д.), для которых только и выполняется извлечение квадратного корня в целых числах с получением соизмеримых отношений p^2/q^2, то можно привести сколь угодно много доказательств несоизмеримости √2. Однако √2 =1,414… является десятичной дробью, а не целым числом, следовательно, для утверждения о непериодичности дроби 1,414… тривиального доказательства несоизмеримости в целых недостаточно.

Мы ввели в рассмотрение бесконечные десятичные дроби, поэтому для всех целых чисел появилось сразу несколько эквивалентных записей — как минимум две, с периодом (9) и с периодом (0). При этом мы договорились, что 1,(9)=2, хотя число 1,(9) — это бесконечная десятичная дробь, а 2 — целое число. То есть в современной арифметике действует еще одна аксиома, согласно которой в определенных случаях десятичная дробь (нецелое бесконечное приближение к целому) эквивалентна целому числу!

Допустив однажды, что дробь может быть равна целому числу, в доказательстве иррациональности √2 возникает потребность в обосновании того факта, что для √2 невозможно подобрать и такое дробное значение, которое можно принять за эквивалентное целому. Для этого нужно ответить на вопрос: на основании чего вообще была введена столь смелая аксиома эквивалентности дроби и целого числа? Оказывается, на основании правил перевода десятичных дробей в обыкновенные, которые выполняются не только для всех приближений с недостатком 1,9; 1,99; 1,999 и т.д., но и для всех приближений с избытком 2,1; 2,01; 2,001 и т.д., тогда мы можем записать:

2,(0)=1,(9)=(20–1–(2–1))/9=18/9=2;

2,(0)=2,000…1=(20+1–(2+1))/9=18/9=2.

Из этих записей следует, что каждое значение с недостатком –μn, а также каждое значение с избытком +μn, являются конечными десятичными приближениями к целому числу 2 и к соответствующей точке на числовой прямой. Если десятичная дробь 1,414… имеет период, который при возвышении данной дроби в квадрат, дает решение Δ^2 в десятичных значениях, эквивалентных целому числу 2, то среди конечных последовательностей дроби 1,414… должно содержаться решение δ^2, удовлетворяющее одному конечному значению –μn, +μn из приближений –M, +M (с недостатком или избытком) к целому числу 2.

В этом случае уже нельзя делать категорических заявлений, будто в бесконечной десятичной дроби 1,414… не может содержаться ни одного конечного решения δ^2, из которого можно получить конечное приближение –μn, +μn `in` –M, +M → Δ^2. Потому что конечные числа вида 1414_707_ – 1414_, получаемые в числителе обыкновенной дроби p /q, после их возведения в квадрат будут давать приближения, по разрядности соответствующие числу 199_700000_1000_. После сокращения нулей (со знаменателем дроби 99_800_1000000_) мы получим число вида 199_700000_1, которое оканчивается на 1. Получить единицу на конце такой последовательности уже можно. Например, при возведении в квадрат конечной последовательности, оканчивающейся либо на единицу ( _1^2=1), либо на девятку ( _9^2=81).

Другими словами, число вида 199_600_2, которое мы ввели в тривиальном доказательстве несоизмеримости оказывается не единственным искомым числом в арифметике, где действует аксиома эквивалентности дроби и целого. Если принять лишь тривиальное доказательство, в котором подразумевается, что p^2/q^2 может быть равно либо целому числу, либо эквивалентной дроби с недостатком –μn, то мы вновь придем к некорректному применению принципа «tertium non datur».

Подразделение на соизмеримые и несоизмеримые отрезки всегда лишало Евклидову геометрию логической стройности. М.Я. Выгодский писал об этом следующее: «Тягостность этого подразделения хорошо известна всем изучавшим геометрию и преподававшим ее. Создавая видимость строгости, оно не дает ни логического, ни эстетического удовлетворения. Его искусственность усугубляется тем, что соизмеримые и несоизмеримые отрезки геометрически совершенно равноправны» ^{[32, С.283]}.

В самом деле, выбор эталона длины происходит произвольным образом, поэтому ничто не мешает принять диагональ некоторого квадрата, скажем, за единичный отрезок, которым будут произведены те или иные измерительные работы. Получается, что одна и та же геометрическая величина (отрезок) может иметь различную арифметическую природу в зависимости от того, как ее представляет себе человек. Такой подход равносилен тому, как если бы геометр обладал знаниями, позволяющими ему на свое усмотрение заставлять двигаться солнце вокруг земли или, наоборот, заставлять землю обращаться вокруг солнца.

Расширенная аксиома эквивалентности снимает это «тягостное» затруднение, показывая, что числовые последовательности несводимых к целым числам квадратов и целые числа могут быть выражены через общее представление о периодических десятичных дробях, а значит, имеют единую арифметически упорядоченную природу. На справедливость данного подхода указывает и введенная Д. Гильбертом первая аксиома порядка: «Если А,В,С — точки одной прямой, и В лежит между А и С, то В лежит также между С и А». По мнению М.Я. Выгодского в геометрии нет особой надобности вводить такое тафтологическое определение понятия «между» и специально оговаривать, что фраза «В лежит между А и С» равносильна фразе «В лежит между С и А» ^{[32, С.267]}.

И все же в арифметике эта «очевидность» уже не столь очевидна, как в геометрии. Если обозначить точки А,В,С, лежащими на одной прямой через целые числа, то окажется, что в стандартной математике, оперирующей только бесконечными приближениями с недостатком –μn, непрерывный переход между ними будет осуществляться лишь в направлении от А к В, так как для непрерывного перехода от С к В нужны симметричные им бесконечные приближения с избытком +μn .

Помимо проблемы непрерывности (континуума), а также смежной проблемы объединения геометрической величины и арифметического числа, интуиционистский подход к разрешению второй проблемы Д. Гильберта позволяет по-новому взглянуть на старую проблему бесконечно малых величин.

Топологическое разбиение n-мерных объектов на элементы той же размерности (брауэрово разбиение) позволяет обнаружить периодические десятичные значения у класса чисел, которые в стандартной математике принимаются как дроби, не имеющие периодов. Например, для √2 можно записать следующее отношение двух целых чисел m ^2/n^2:

(I)

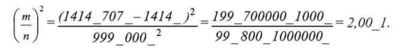
Брауэрово разбиение для кубического корня из 2 выполняется по аналогии с разбиением для квадрата. Объем для удвоенного куба выразится формулой: 2n^3–(2n^2–1), где n — число элементов стороны базисного куба. Разумеется, как в случае с удвоением квадрата, мы будем получать по этой формуле только последовательные приближения к удвоенному кубу. Невозможность решения задачи по удвоению куба в целых числах была доказана давно. Но нам и не требуется решение в целых числах, нас интересуют только приближения для удвоенного куба по десятичным кубам 10^3, 100^3, 1000^3 и т.д., которые позволяют получить число, стоящее до начала периода в десятичной дроби 1,259_432_432_(432_). Тогда мы получим следующие объемы:

2·10^3–(2·10^2–1) = 1801; 2·100^3–(2·100^2–1) = 1980001; 2·1000^3–(2·1000^2–1) = 1998000001 и т.д.

Разрядность этих приближений в целых совпадает с разрядностью, получаемой на каждом шаге приближения дроби (2^1/3=1,259…)^3, а именно на первом шаге для дробных имеем 1,728, а для целых 1801. На втором шаге для дробных 1,953125, а для целых 1980001. На третьем шаге для дробных 1,995616979, а для целых 1998000001 и т.д. Таким образом, можно получить следующее отношение двух целых чисел m^3/n^3:

(II)

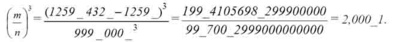
На что следует обратить внимание, так это на то, что в выражениях (I) и (II) значение для квадратного корня (2,00_1) по разрядности отличается от значения для кубического корня (2,000_1). Различия эти задают разницу в записях (2^1/2)^2 =2 и (2^1/3)^3=2. Разницу, которая никак не учитывается в формулах стандартной математики, отчего можно прийти к ошибочному умозаключению, будто между пространствами различных размерностей существует непрерывный переход, так как все несводимые к целым числам корни из числа 2 оказываются в таких записях равными одной и той же десятичной дроби с периодом (9): (2^1/2)^2 =1,99(9)=2; (2^1/3)^3=1,99(9)=2 и т.д. Именно поэтому Г. Кантор, ради удобства выбрасывавший из рассмотрения десятичные дроби с периодом (9) и прекративший «бесцельные» исследования бесконечно малых величин, сумел получить свое знаменитое «патологическое доказательство», согласно которому сторона квадрата (1-мерное пространство) и его площадь (2-мерное пространство) равны по числу точек, то есть равномощны или топологически эквивалентны.

Вопреки убеждениям Эйлера, в бесконечно малых величинах, к которым стандартная математика привыкла относиться с пренебрежением, все-таки содержатся некие «глубокие таинства». Ответ на вопрос, что это за «таинства», позволяет получить перенос интуиционистских идей Л. Брауэра из топологии в арифметику, в результате чего становится возможно эффективное упорядочение таких последовательностей, которые до этого рассматривались как эффективно неупорядоченные или хаотичные. Обнаружение этих закономерностей полностью согласуется с результатом П. Коэна, который в 1963 году доказал, что ни проблема континуума, ни возможность упорядочения любого бесконечного множества (аксиома выбора Леви-Цермело) не зависят от системы аксиом стандартной математики.

В связи с этим необходимо заметить, что упорядочение последовательностей несводимых к целым числам радикалов можно рассмотреть с точки зрения теоремы Абеля-Руффини и теории Э. Галуа о неразрешимости в радикалах уравнений пятой степени и выше. В самом деле, почему корни уравнений ниже пятой степени можно выразить в радикалах, а уравнений пятой степени и выше — нет? Поиск ответа на этот вопрос стимулировал появление глубоких математических теорий и исследований. Академик РАН В.И. Арнольд обнаружил, что алгебраические уравнения пятой степени и выше не решаются в радикалах по топологическим причинам ^{[33, С.4]}.

Зная о том, что для получения радикала любой n-степени должен выполняться какой-то один способ для упорядочения получаемой последовательности, можно заключить, что, начиная с пятой степени, таких способов становится несколько. Например, пятую степень можно представить в виде суммы степеней 2+2+1 либо 2+3, причем во втором случае порядок последовательности задается двумя различными способами (ведь топологический порядок первой степени в случае 2+2+1, задающийся на числовой прямой, совместим с топологическим порядком любой размерности). Для упорядочения таких неопределенных последовательностей, появляющихся в уравнениях пятой степени и выше, необходимо вводить дополнительные правила, которые ограничивают возможности внутренних преобразований при упорядочении знаков последовательностей, что ведет, в том числе, к ограничению возможных преобразований между членами уравнений, то есть как раз к явлению невыразимости.

LVMEN RATIONALIS

Философско-математическая концепция интуиционизма позволяет не только дать более удачную рациональную реконструкцию трех кризисов в основаниях математики, показать их общие корни, а также искажения реальной истории науки, связанные с установлением теоретико-множественной парадигмы, она позволяет обнаружить математический ключ к негативному решению второй проблемы Д. Гильберта, которая была сформулирована в 1900 году на II Международном Конгрессе математиков. Несмотря на то, что сам Д. Гильберт пытался отыскать доказательство непротиворечивости системы аксиом стандартной арифметики, негативное решение данной проблемы в полной мере подтверждает его убежденность в неограниченных возможностях познания, ибо в математике не существует тезиса «ignoramus et ignorabimus» (c лат. «мы не знаем и никогда не узнаем») ^{[26, С.22]}.

Кроме того, решение второй проблемы Д. Гильберта, которое было признано многими математиками практически неосуществимым после публикации статьи К. Геделя «О формально неразрешимых предложениях Principia Mathematica и родственных систем» (1931 г.) , подтвердило другие слова Д. Гильберта о том, что у сложных проблем не обязательно должно быть сложное решение, что «строгие методы являются в то же время простейшими и наиболее доступными» ^{[26, С.17]}. Как показывает язык античной геометрии, языки анализа и теории множеств, за введением новых аксиом и усложнением символизма могут скрываться неразрешенные антиномии, отложенные «в долгий ящик». Как остроумно высказался в рецензии на книгу Умберто Эко «Кант и утконос» английский математик Саймон Блэкберн: «Противоречивость есть вещь упорная; вы можете избавиться от нее не добавлением, а лишь отниманием» ^{[34, С.133]}.

Философию интуиционизма можно представить именно таким «отниманием» у стандартной математики теории несоизмеримых отрезков, некорректного применения принципа «tertium non datur», аксиомы Г. Кантора о двух стягивающихся в общую точку отрезках и других важных элементов-подпорок, необходимых для «выживания» теории множеств. Однако не стоит представлять обнаружение противоречий в системе аксиом арифметики как революционный призыв к разрушению грандиозного здания стандартной математики или как хирургическое вмешательство, которое потребовалось изношенному старческому организму.

Речь следует вести об очень длительной и драматической эволюции математических теорий, в результате которой выделился принципиально иной вид теорий, имеющий в своем распоряжении более эффективные инструменты познания, обладающий во многом еще неизвестными способностями и готовый к сосуществованию с другими видами теорий. Интуиционизм раздвигает границы мышления, позволяет увидеть закономерности там, где стандартные теории впадают в неопределенность. В нем история науки перестает быть пассивным регистратором накопления знаний, но само время начинает выступать в качестве создателя нелинейной внутренней логики возникновения научных открытий, в полном соответствии с интуиционистскими взглядами И. Лакатоса ^[35].

Развивая мысль А.Н. Колмогорова о соотношении истинной математики и «псевдоматематики», выдающийся логик Г. Чейтин указал на существование предела для каждой достаточно богатой теории, не позволяющего выводить для объекта x колмогоровской сложности (самой малой длины совокупности знаков, описывающей данный объект) некий универсальный алгоритм, адекватно отражающий совокупность всех знаков для полного описания данного объекта.

В отличие от арифметики, где довольствуются записью (2^1/2)^2 =1,99(9)=2 с нетривиальным утверждением о непериодичности дроби 1,414… и столь же нетривиальным утверждением об эквивалентности дроби и целого числа, в интуиционистской арифметике такой записи соответствует подробный разбор приближений, в котором для объекта x (дробь √2=1,414…) обнаруживается топологически обусловленное свойство упорядоченности. Предел Чейтина, заложенный в философии интуиционизма, значительно превосходит познавательный предел стандартной математики.

Понятие потенциальной бесконечности позволяет выходить, вообще говоря, за рамки любых финитных символов. Поэтому интуиционизм вполне терпимо относится к теологическим и философским вопросам, воспринимая символы религиозной парадигмы как семантику, применяемую человеком во всех языковых системах. И нет ничего странного в том, что некоторые выдающиеся ученые XX века проявляли интерес к мистике, в том числе, математики Г. Кантор и Л. Брауэр. Однако любая религиозная парадигма, выражаемая знаками того или иного священного писания, тоже не есть некий абсолютный познавательный предел для интуиционизма.

Исключение тех или иных символов, с помощью которых человек стремится отобразить истину, допустимо лишь тогда, когда они не могут быть верно интерпретированы в грубых схемах рассудочной деятельности. Но если разум достаточно подготовлен, интуиция может открыть ему мир непрерывных аналогий, которые окружают нас всюду, которые содержатся внутри нас, из которых состоит сам разум. И этот мир отнюдь не будет застывшей теорией, которой разум может только «служить». Такая возможность совместного «служения» и «направления» перекликается с символом Знания, которое открывает Агнец в Откровении Иоанна Богослова, после чего двадцать четыре старца и тетраморф нарекают себя «царями и священниками Богу». Ведь это очень точное описание интуиции! Так или иначе, она присуща каждому из нас, она и есть естественная среда разума, то информационное поле, которое человек видоизменяет и возделывает, но которое само оказывает на него воздействие, приближая сквозь время великие озарения и открытия.

Философия интуиционизма имеет огромные познавательные перспективы, которые могут применяться во всех областях знаний, но будет ли она востребована в мире, где господствует парадигма формализма, рассматривающая человека в качестве биологическо-социальной машины, выполняющей лишь некие конечные, исключительно «земные» программы, или в мире, где господствует культура Вырождения, опускающая человека до животного состояния, уничтожающая в подрастающем поколении такие понятия как «совесть», «нравственность», «доброта», «человеколюбие»? Думается, что вряд ли в такой агрессивной среде сможет вырасти и прижиться принципиально иное, отличное от всего нам до сих пор известного, миропонимание. И все-таки к этому стоит стремиться, потому что философия интуиционизма в широком смысле слова и есть такой путь развития творческих способностей, который позволяет избежать негативных и губительных для всего живого проявлений современной культуры.

You can simply select and copy link from below text field.